Мастер работая самостоятельно, может изготовить партию из 200 деталей за некоторое время. ученик за - id11320920220904 от Владушкаcat 04.09.2022 04:59

Question

Алгебра: Мастер работая самостоятельно, может изготовить партию из 200 деталей за некоторое время. ученик за это время может изготовить только половину всех деталей. работая вместе, они могут изготовить всю партию деталей за 4 часа. за какое время мастер может изготовить все детали, работая самостоятетьно?

Владушкаcat · Accepted Answer

За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:

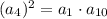
$(a_4)^2=a_1 \cdot a_{10}$

Використаємо формулу 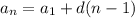a_n=a_1+d(n-1) :

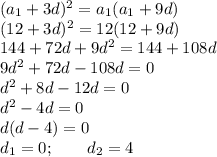
$(a_1+3d)^2=a_1(a_1+9d)\\(12+3d)^2=12(12+9d)\\144+72d+9d^2=144+108d\\9d^2+72d-108d=0\\d^2+8d-12d=0\\d^2-4d=0\\d(d-4)=0\\d_1=0; \qquad d_2=4$

Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.

Другий варіант:

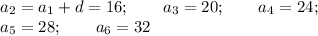
$a_2=a_1+d=16; \qquad a_3=20; \qquad a_4=24;\\a_5=28; \qquad a_6=32$

До речі, перевіримо:

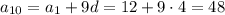
$a_{10}=a_1+9d=12+9 \cdot 4=48$

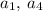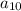Бачимо, що $a_1, \: a_4$ та $a_{10}$ справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.

Відповідь. Умові задовольняють дві прогресії:

1) 12, 12, 12, 12, 12, 12.

2) 12, 16, 20, 24, 28, 32.

MOGZ ответил