а) целые: 423/3; -2√4; 0
б) рациональные: -3,1; 423/3; 7,(1); -2√4; 0
Объяснение:
Целые числа - это числа не имеющие дробную часть. Это все натуральные числа, число ноль и числа, противоположные натуральным числам.
Поэтому, среди представленных чисел натуральными числами являются: 423/3; -2√4; 0
423/3 = 141 - т.к. это натуральное число
-2√4 = -2*2 = -4 - т.к. это число противоположное натуральному числу 4.
Рациональные числа – это те, которые можно представить в виде где числитель m — целое число, а знаменатель n — натуральное число. Это все натуральные, все целые числа, все обыкновенные дроби, все бесконечные периодические дроби и все конечные десятичные дроби.
Поэтому, среди представленных чисел рациональными числами являются:
-3,1; 423/3; 7,(1); -2√4; 0
-3,1 - т.к. это конечная десятичная дробь
423/3 =41 - т.к. это целое число
7,(1)=7,1111 - т.к. это бесконечная периодическая дробь
-2√4 = -2*2= -4 - т.к. это целое число
0 - т.к. это целое число
*** Число √18=√(3²*3) = 3√3 - не является рациональным числом. Это число иррациональное.
2.
...; 0,12; 0,6; x; 15; ... - геометрическая прогрессия
Очевидно, что все члены положительны, значит, ОДЗ: x>0
Числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого члена, кроме первого и последнего, равен произведению предыдущего и последующего членов.
OТВЕТ: 3
3.
1)
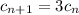
2) С формулы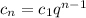
проверим число
Число 45 не является степенью числа 3, т.е. 45 нельзя представить в виде степени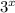
с натуральным показателем 
, значит,
число 225 не является членом данной прогрессии.
3) Проверим число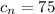
=> 
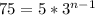
Число 55 не является степенью числа 3 с натуральным показателем, значит,
число 75 не является членом данной прогрессии.
3) Проверим число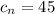
=> 
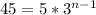
Число 45 является третьим членом данной прогрессии.
4) Проверим число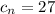
=> 
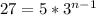
Число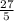
не является степенью числа 3 с натуральным показателем, значит, число 27 не является членом данной прогрессии.
ответ: 45.