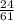проте ймовірність того, що листок містить саме число 2 менша та дорівнює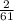 
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події 
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише 
, оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме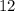 
1)x=±1; (тут просто выносим 4 и выходит 4*(x^2-1)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
2) x=-19/8; 1 (тут просто по дискриминанту)
3) x ничему не равняется еле же x=±6i (число в квадрате не может быть меньше нуля, ну а если решать на комплексных числах то x=±6i)
4) x=-4; x=-1 (по теореме Виета, еле по дискриминанту)
5) x=4 (можно сгрупировать еле по дискриминанту)
6) x=1/5; x=2 (по дискриминанту)
7) x=1/5; x=4 (по дискриминанту)
8) x ничему не равняется еле же x=(3±i√191)/20 (тут дискриминант меньше нуля будет, поэтому если решение и есть то оно на площади комплексных чисел)
9) x=-7; x=0; (выносим x и выходит x*(x+7)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
10)x=±0.5; (тут просто выносим 64 и выходит 64*(1/4-t^2)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
11) x=1; x=5/3; (по дискриминанту)
12) x ничему не равняется еле же x=±i*√15 ( можно вынести минус и тогда выйдет -(15+x^2)=0 число в квадрате не может быть меньше нуля, ну а если решать на комплексных числах то x=±i*√15)
13) x=-1; x=4/5 (по дискриминанту)
14) x=-6; x=5 (по теореме Виета, еле по дискриминанту)
15) x=2/3; (по дискриминанту)
16) y=2/5; y=1/2 (по дискриминанту)
17) x=6/5; x=2 (по дискриминанту)
18) x ничему не равняется еле же x=( -1±i*√(19) )/10 ( Дискриминант меньше нуля соответственно решение есть только на комплексных числах то x=( -1±i*√(19) )/10;
19) x=0; x=0.5 (тут просто выносим 4x и выходит 4x*(0.5-x)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
Поскольку D>0 для любого значения a --> уравнение имеет 2 действительных корня.
ответ: 2 действительных корня.