Это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. Она тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний.
Теория вероятностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.
Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:
Дискретная случайная величина — величина, которая в результате испытания может принимать определенные значения с определенной вероятностью, то есть образовывать счетное множество.
Элементы множества можно пронумеровать. Они могут быть как конечными, так и бесконечными. Например: количество выстрелов до первого попадания в цель.
Непрерывная случайная величина — это такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Количество возможных значений непрерывной случайной величины бесконечно.
Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.
Вероятностное пространство — это тройка (Ω, Σ, Ρ) иногда обрамленная угловыми скобками: ⟨ , ⟩ , где
Ω — это множество объектов, которые называют элементарными событиями, исходами или точками.
Σ — сигма-алгебра подмножеств , называемых случайными событиями;
Ρ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .
ответ: 4.
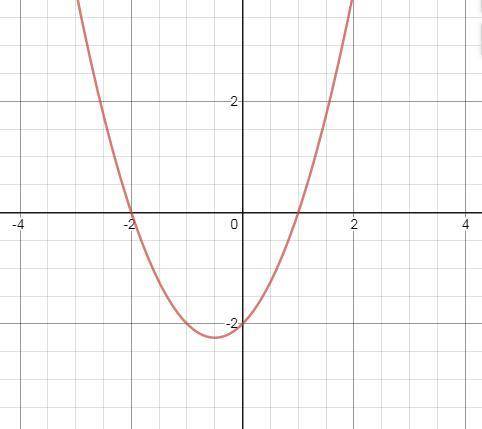
Объяснение: Для начала построим график функции y = x² + x - 2
ординаты вершины: 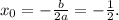 ,
, 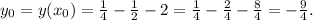
Координаты точек пересечения с осями координат:
1) с ОХ: у = 0. x² + x - 2 = 0. По теореме Виета х₁ = 1, х₂ = -2. (1; 0), (-2; 0)
2) с ОУ: х = 0. у(0) = 0 + 0 - 2 = -2. (0; -2).
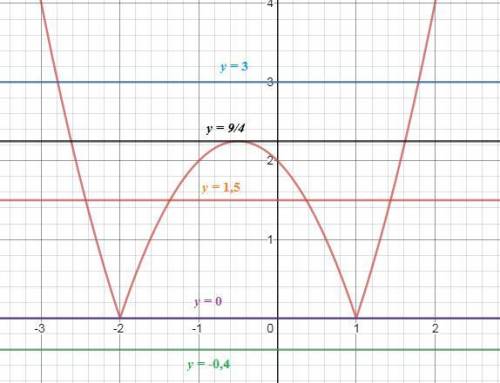
График - во вложении 1.
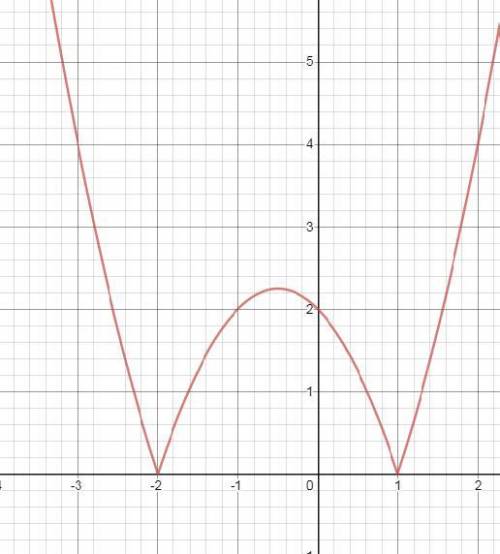
Из графика y = x² + x - 2 можно получить график функции y = |x² + x - 2|, если ту часть графика, которая ниже оси ОХ, "отзеркалить" относительно оси ОХ. В итоге получим график во вложении 2.
Прямая, параллельная оси абсцисс, имеет вид y = a, где а - произвольное число. Будем подбирать разные значения параметра а и посмотрим, какое максимальное кол-во общих точек будут иметь наша функция и прямая y = a. (вложение 3)
Если а < 0 (наглядный пример - а = -0,4), то общих точек не будет вообще.
Если а = 0 (прямая совпадает с осью ОХ), то имеем ровно две точки пересечения.
Если а = 9/4 (отзеркаленная вершина), то иметь будем 3 точки пересечения. А если брать промежуточные значения - 0 < a < 9/4 (наглядный пример - а = 1,5), - то будет 4 точки пересечения, т.е. 4 общих точки.
Если брать значения а > 9/4 (наглядный пример - а = 3), то у нас будет только 2 общих точки.
Итого: наибольшее число общих точек графиков наших функций - 4.
........................