1. Строим на координатной плоскости два графика:
y = -6-x
y = 8/x
Первый представляет прямую. Можно построить по двум точкам (0; -6) и (-6; 0) (точки получились подстановкой по очереди x=0 и y=0)
Второй график -- гипербола. Также строим по точкам:
(-4; -2), (-2; -4). (2; 4), (4; 2) (можно подставить ещё x=-8; -1; 1; 8)
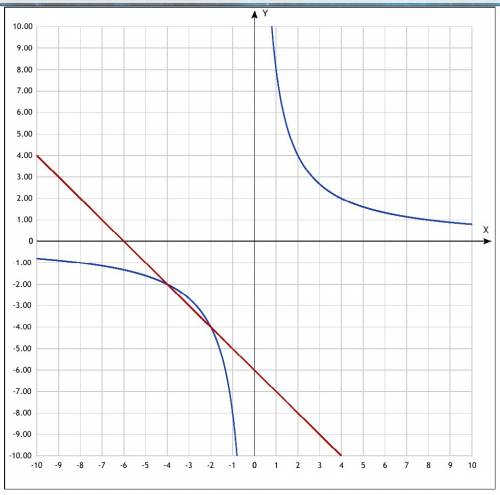
Во вложении представлены эти графики. Синий -- график функции y = 8/x, красный -- y = -6-x
2. Находим точки пересечения графиков на координатной плоскости и записываем их координаты:
(-4; -2) и (-2; -4)
Это и есть ответ для уравнения 8/x = -6-x
ответ: (-4; -2) и (-2; -4)
Объяснение:
Пусть длина равна х, а ширина - у. Тогда периметр прямоугольника равен 2*х+2*у, а площадь - х*у
Получаем систему:
2*х+2*у=26
х*у=42
2х+2у=26
2*(х+у)=26 (Делим обе части на 2)
х+у=13
Тогда х=13-у, представим х в нижнее выражение:
(13-у)у=42
13*у-у^2=42 (Перенесем все в правую часть(
у^2-13*у+42=0
Дискриминант =169-168=1, Дискриминант >0, 2 корня
у1=(13+1)/2=7
у2=(13-1)/2=6
Подставим в уравнение х+у=13 получившиеся значения и найдём х1 и х2 соответственно
х1+у1=13
х1+7=13
х1=6
х2+у2=13
х2+6=13
х2=7
Стороны прямоугольника равны 6 и 7