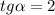В решении.
Объяснение:
7. Упростить:
(х√у - у√у)/2 * [√х/(√х + √у) + √х/(√х - √у)]= х√у.
1) [√х/(√х + √у) + √х/(√х - √у)]=
общий знаменатель (√х + √у)(√х - √у), надписываем над числителями дополнительные множители:
=[(√х - √у) * √х + (√х + √у) * √х] / (√х + √у)(√х - √у)=
=(х - √ху + х + √ху) / (√х + √у)(√х - √у)=
в знаменателе развёрнута разность квадратов, свернуть:
= 2х/(х - у);
2) Умножение:
(х√у - у√у)/2 * 2х/(х - у)=
=[√у(х - у)]/2 * 2х/(х - у)=
=[√у(х - у) * 2х] / [2 * (х - у)]=
сократить (разделить 2 и 2 на 2, (х - у) и (х - у) на (х - у):
= х√у.
8. Дана функция y=√x
а) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
у=√х
1) А(63; 3√7)
3√7 = √63
3√7 = √9*7
3√7 = 3√7, проходит.
2) В(49; -7)
-7 = √49
-7 ≠ 7, не проходит.
3) С(0,09; 0,3)
0,3 = √0,09
0,3 = 0,3, проходит.
б) х∈ [0; 25]
y=√0 = 0;
y=√25 = 5;
При х∈ [0; 25] у∈ [0; 5].
в) Найдите значения аргумента, если у∈ [9; 17]
у = √х
9=√х х=9² х=81;
17=√х х=17² х=289.
При х∈ [81; 289] у∈ [9; 17].
1) Пусть х° - градусная мера 1 части, тогда
3х - градусная мера внешнего ∠А;
4х - градусная мера внешнего ∠В;
5х - градусная мера внешнего ∠С
2) Так как внешний и внутренний углы при одной вершине - смежные, то их сумма равна 180°.
Получаем внутренние углы ΔАВС
(180°-3х) - градусная мера внутреннего ∠А;
(180°-4х) - градусная мера внутреннего ∠В;
(180°-5х) - градусная мера внутреннего ∠С
3) Так как сумма внутренних углов любого треугольника равна 180°, получаем уравнение для внутренних углов ΔАВС.
(180°-3х) + (180°-4х) + (180°-5х) = 180°
-12х = 180° - 540°
- 12х = - 360°
х = - 360° : (-12)
х = 30° градусная мера 1 части.
4) 180°-30° · 3 = 90° - градусная мера внутреннего ∠А;
180°-30° · 4 = 60° - градусная мера внутреннего ∠В;
180°-30° · 5 = 30° - градусная мера внутреннего ∠С
5) ∠А : ∠В : ∠С = 90° : 60° : 30°
Сократим на 30.
90 : 60 : 30 = 3 : 2 : 1
ответ В) 3 : 2 : 1
1)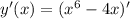
2)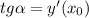
ответ: