Question

Определи абсциссу вершины параболы, проходящей через точки c координатами (0;−6), (5;1), (−5;−1)
ответ округли до десятых​

Answer 1

ответ: абсцисса вершины параболы = 0.

Объяснение:

(0;-6)    (5;1)    (-5;-1)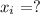      $x_{i}=?$

Координата х вершины параболынаходится по формуле:

$x_{i}=-\frac{b}{2a} .$

Уравнение параболы в общем виде:

$ax^{2} +bx+c=0$

Подставляем координаты точек, через которые проходит парабола

в уравнение параболы в общем виде:

{a*0²+b*0+c=-6         {c=-6

{a*5²+b*5+c=1            {25a+5b-6=0

{a*(-5)²+b*(-5)+c=-1     {25a²-5b-6=0

Вычитаем из второго уравнения третье:

10b=0

b=0   ⇒

$x_{i} =-0/2a=0.$