54 варианта.
Объяснение:
По 2 натуральных слагаемых:
7 = 6+1 = 5+2 = 4+3 = 3+4 = 2+5 = 1+6
6 вариантов.
По 3 натуральных слагаемых:
7 = 5+1+1 = 4+2+1 = 4+1+2 = 3+3+1 = 3+2+2 = 3+1+3 = 2+2+3 = 2+4+1 = 2+3+2 = 2+1+4 = 1+3+3 = 1+2+4 = 1+4+2 = 1+5+1 = 1+1+5
15 вариантов.
По 4 натуральных слагаемых:
7 = 4+1+1+1 = 3+2+1+1 = 3+1+1+2 = 3+1+2+1 = 2+2+2+1 = 2+2+1+2 = 2+1+2+2 = 1+3+1+2 = 1+3+2+1 = 1+2+3+1 = 1+2+1+3 = 1+1+2+3 = 1+1+3+2 = 1+2+2+2 = 1+1+1+4
15 вариантов.
По 5 натуральных слагаемых:
7 = 3+1+1+1+1 = 2+2+1+1+1 = 2+1+2+1+1 = 2+1+1+2+1 = 2+1+1+1+2 = 1+2+2+1+1 = 1+2+1+2+1 = 1+2+1+1+2 = 1+1+2+1+2 = 1+1+2+2+1 = 1+1+1+2+2
11 вариантов.
По 6 натуральных слагаемых:
7 = 2+1+1+1+1+1 = 1+2+1+1+1+1 = 1+1+2+1+1+1 = 1+1+1+2+1+1 = 1+1+1+1+2+1 = 1+1+1+1+1+2
6 вариантов.
По 7 натуральных слагаемых:
7 = 1+1+1+1+1+1+1
1 вариант.
Всего 6+15+15+11+6+1 = 54 варианта.
1.
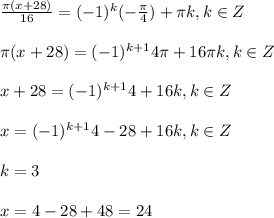
наименьший положительный х=24
2.
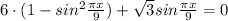
Квадратное уравнение относительно синуса
6t²-√3·t-6=0
D=3+144=147
√D=√(3·49)=7·√3
t₁=-√3/2; t₂=2√3/3 > 1
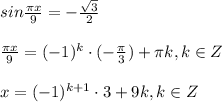
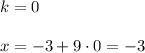
наибольший отрицательный
4.
Так как
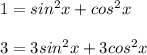
уравнение имеет вид:
2cos²x+6√3sinx·cosx+3sin²x+3cos²x=0
3sin²x+6√3sinx·cosx+5cos²x=0
Это однородное тригонометрическое уравнение.
Делим на cos²x≠0
3tg²x+6√3tgx+5=0
D=(6√3)²-4·3·5=108-60=48
√D=4√3
tgx=-5√3/3 или tgx=-√3/3
x=arctg(-5√3/3) +πk, k∈Z или x=arctg(-√3/3)+πn, n∈Z
Функция y=arctgx - монотонно возрастающая на (-∞;+∞)
-(5√3/3) < (-√3/3)⇒arctg(-5√3/3) < arctg(-√3/3)
Наибольший отрицательный
n=0
x=atctg(-√3/3)=-30°
0,29
Объяснение:
Количество выбрать 4х учеников из 15 определяется по формуле сочетаний С(n, k)=n! / k!*(n-k)! :
выбрать 4х учащихся из 15;
выбрать 3х спортсменов из 8 можно С при этом 1 из 4х должен не быть спортсменом, его можно выбрать С Число событий благоприятствующих выбору 3х спортсменов из 4х равно С(8,3)*С(7,1):
C(8,3)=8! / 5!*3! = 56 ; C(7,1)=7! / 6!*1! = 7 ; С(8,3)*С(7,1)=56*7=392 ; P=392/1365=56/195=0,29