Объяснение:
у = sin(x)
Область определения: D(f) = (-∞; +∞) или D(f)∈RОбласть значения: E(f) = [-1; 1]Нули функций: x₀ = πn, n∈ZЧетность функций: sin(-x) = -sin(x) - нечетнаяПериод функций: sin(x+T) = sin(x) ⇒ T = 2πПромежутки монотонности:y = sin(x)↑ на [-π/2 + 2πn; π/2 + 2πn], n∈Z
y = sin(x)↓ на [π/2 + 2πn; 3π/2 + 2πn], n∈Z
Промежутки знакомо постоянства:y>0 при x∈(0 + 2πn; π + 2πn), n∈Z
y<0 при x∈(π + 2πn; 2π + 2πn), n∈Z
Наибольшее и наименьшее:y = 1 - наибольшее при x = π/2 + 2πn,n∈Z;
y = -1 - наименьшее при x = − π/2 + 2πn,n∈Z;
Обратимость: y = arcsin(x) на [- π/2; π/2]Ограниченность: Ограничена сверху и снизуПроизводная: y = (sin(x))' = cos(x)График: (показано внизу)↓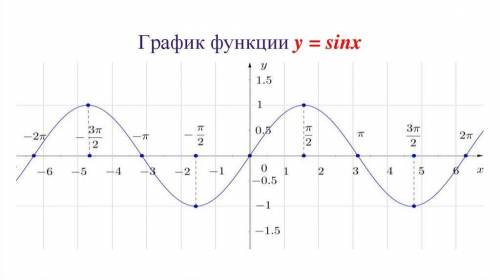
На второй полке 32 книги, на третьей полке 40 книг.
Объяснение:
Будем считать, что в вопросе задачи опечатка, и требуется вместо яблок в корзинах найти количество книг на второй и третьей полках. Поэтому, так как по условию нам сказано, что на первой полке стоит 36 книг, а количество книг на второй полке составляет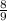 
от количества книг на первой полке, поэтому приняв количество книг на первой полке за единицу а количество книг на второй полке за икс, составим пропорцию:
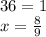
Откуда, принятое за x количество книг на второй полке будет равно:
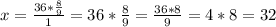книги на второй полке.
И эти 32 книги будут составлять 80% от количества книг на третьей полке, поэтому составляем еще одну пропорцию, приняв количество книг на третьей полке за 100%:
%
%
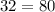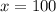Аналогичным решения пропорции "крест на крест", находим количество книг на третьей полке:
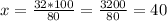книг на третьей полке.
Получаем ответ: на второй полке 32 книги, на третьей полке 40 книг.
1)L = 2пR => радиус окружности = 1
Правильный шестиугольник можно разбить на 6 треугольников, которые будут равнобедренные, т. к. Их боковые стороны будут являться радиусами окружности. Если мы найдём третью сторону треугольника, то поймём, что они ещё и равносторонние,т.е. все равны 1 см. Из этого можно сделать вывод, что сторона шестиугольника = 1 см и его периметр равен 6
ответ: Д
2) S = 1/2 * ah ; 24 = 1/2 * 6 * h ; h= 24 :(1/2*6) = 8
Т.к. У нас треугольник прямоугольный => высота - это второй катет
По т. Пифагора:
6²+8²= с²
с = √(36+64) = √100 = 10
Известно, что гипотенуза прямоугольного треугольника является диаметром описанной окружности => R = 5
Получается L = 2*3*5 = 30, но это длина всей окружности
Составим пропорцию:
30 - 360°
Х - 200°
Х = (200*30)/360 = 16 2/3 см
ответ: Длина дуги = 16 2/3 см
3) S = пR² - площадь описанной окружности
S = пr² - площадь вписанной окружности
a = R√3 => R = a/√3
r = a/(2*√3) => r = R/2
S впис. окр. = п * (R/2)² = (пR²)/4
S опис. окр. / S впис. окр. = (пR²)/4 : пR² = (пR²)/4 * 1/(пR²) = 1/4
ответ: S опис. окр. / S впис. окр. = 1/4