II вариант:
Обязательная часть.
А1. Решите систему неравенств
На каком из рисунков изображено множество её решений?
ответ: ___
А2. При каких значениях х функции у = 2х -6 и у = 5х + 3 принимают положительные значения?
Варианты ответов:
1) (-0,6; +∞)
2) (-∞; -0,6)
3) (3; +∞)
4) (-0,6; 3)
ответ: ___
А3. Укажите решение системы неравенств
х < 9
8 -х > 0
Варианты ответов:
1) (8; +∞)
2) [-1,1; +∞)
3) (8; 9)
4) (-∞; 9)
ответ: ___
А4. Какие из чисел не являются решением системы неравенств
2х ≥ 6
1 + х > 3
Варианты ответов:
1) 1
2) 2
3) 3
4) 4
ответ: ___
Дополнительная часть.
В1. Решите систему неравенств
Х + 27 < 4х – 18
6-2х < 1,5х -1
Решение:
ответ:
В2. Найдите область определения функции у = –
Решение:
ответ:
Объяснение:
Координаты точки пересечения можно найти методом вычитания:
а)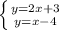 чтобы найти переменную
чтобы найти переменную  , достаточно вычесть от верхней части системы нижнюю, тогда получится
, достаточно вычесть от верхней части системы нижнюю, тогда получится 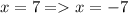 , найдем координату
, найдем координату 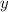 , подставим значение х в любую часть системы:
, подставим значение х в любую часть системы: 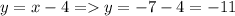 , следовательно точка пересечения этих прямых будет находится по координатам
, следовательно точка пересечения этих прямых будет находится по координатам 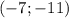
б)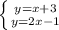
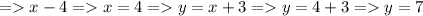 , искомый ответ будет
, искомый ответ будет 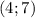
в)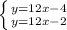 тут возникает противоречие, если прямые вычесть, то мы не сможем найти
тут возникает противоречие, если прямые вычесть, то мы не сможем найти  или
или 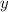 , или же будет
, или же будет 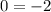 , что не является верным, значит прямые не будут пересекаться, они являются параллельными
, что не является верным, значит прямые не будут пересекаться, они являются параллельными
г)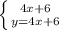 тут уже можно сразу найти
тут уже можно сразу найти  , искомый ответ будет
, искомый ответ будет 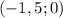
ответ: а)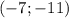 , б)
, б)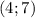 , в)Нет решения, г)
, в)Нет решения, г)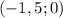
Примечание: Если в г была система такая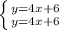 , то это это две прямые, которые совпадают и ответом будет бесконечное множество.
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.