Наиболее сложное решение:
Пусть x - количество бензина в первой бочке, а y - во второй. По условию задачи составим систему уравнений:
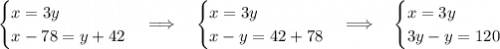
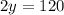
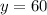 (л) - бензина во второй бочке
(л) - бензина во второй бочке
60 · 3 = 180 (л) - в первой бочке
Решение через уравнение (рационально):
Пусть x - количество бензина во второй бочке, тогда в первой - 3x. По условии задачи составляем уравнение:
3x - 78 = x + 42
3x - x = 42 + 78
2x = 120
x = 60 (л) - во второй бочке
60 · 3 = 180 (л) - в первой бочке
ответ: в первой бочке 180 л бензина, во второй - 60 л.
Задача может быть простой, даже несмотря на тему (здесь нельзя решить сложнее, чем в первом варианте)
В решении.
Объяснение:
Дана функция у = -3х + 2.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 5 2 -1
1) Найти координаты пересечения графиком осей координат.
а) При пересечении любым графиком оси Оу х равен нулю.
у = -3х + 2 х = 0;
у = -3*0 + 2
у = 2;
Координаты точки пересечения графиком оси Оу (0; 2).
б) При пересечении любым графиком оси Ох у равен нулю.
у = -3х + 2 у = 0;
-3х + 2 = 0
-3х = -2
х = -2/-3
х = 2/3;
Координаты точки пересечения графиком оси Ох (2/3; 0).
2) При каких значениях х у > 0 и у < 0?
а) у > 0 (график выше оси Ох) при х∈(-∞; 2/3).
б) у < 0 (график ниже оси Ох) при х∈(2/3; +∞).
3) Возрастающая или убывающая данная функция?
Функция вида у = ах + b;
а < 0, b > 0, функция убывающая.
1) f(x)↓ при х ∈ (-∞; 5]; 2) f(x) ↑ при х∈ [-2; 2]
Объяснение:
1) f'(x) = x - 5 - производная функции
f'(x) < 0 при х ∈ (-∞; 5} на этом интервале функция убывает
2) f(x) = 24x - 2x³ - функция
f'(x) = 24 - 6x² - производная функции
24 - 6х² = 0
х₁ = -2; х₂ = 2
f'(x) > 0 при х ∈ [-2; 2] на этом интервале функция возрастает