Используем формулы привидения
1) если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется;
если же в формуле содержатся углы 90° и 270° (π/2 и 3π/2), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.);
2) чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол φ острым, определить знак выражения, стоящего в левой части формулы.
sin(п-a)/2 cos(п/2+a)
sin(п-a)=sina (во второй четверти sin +)
2 cos(п/2+a)=2(-sina) (во второй четверти cos -)
sina/-2sina=-1/2
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение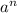 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение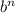 .
.
Рассмотрим многочлен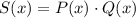 , где:
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена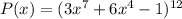 :
:
- степень определяется выражением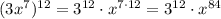 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен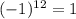
Для многочлена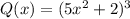 :
:
- степень определяется выражением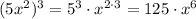 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен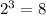
Наконец, для многочлена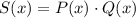 получим:
получим:
- степень определяется выражением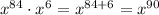 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен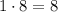
Сумма степени и свободного члена многочлена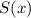 :
:
ответ: 98