1)Множим на син что делиться на син(имеем право домножить потому что син\син =1),умножим чисельник и знаменник на 2
и применим фомулу синуса двойного аргумента (2sinxcosx=2sinx)
Выходит 2sinxcosxcos 2xcos4x
= 2sin2xcos2xcos4x
2sinx = 2sin4xcos4x
4sinx = sin8x
8sinx может ты ошиблась?упустила 8
8sinx
б) умножаем и делим на 4кос кс, сначала на 2 кос кс потом потом просто на 2
2cosxsinx cos2x
=sin2xcos2x
2cosx =*2
2cosx -- = 2sin2xcos2x
2 = sin4x
4cosx
4cosx
в) sinxcos2xcos4x=sin8x\8cosx
множим и делим на 2 cosx, потом 2 раза множим и делим на 2
2sinxcosxcos2xcos4x
= 2sin2xcos2xcos4x
2cosx = 2sin4xcos4x
4cosx = sin8x
8cosx
8cosx
Объяснение:
Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
Теперь предположим что равенство верно для n=k:
Прибавив к обеим частям равенства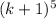 получим:
получим:
Займёмся преобразованием правой части этого равенства:
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.