1. Найдите модуль вектора ⃗(−5;1;2).
А Б В Г
8 30 √30 √8
2. Найдите координаты середины отрезка МК, если М(20;-18;6) и К(-12;-2;4).
А Б В Г
(8;-20;10) (4;-10;5) (-16;-10;5) (8;-10;5)
3. Найдите координаты вектора МК⃗, если М(10;-4;2) и К(16;2;-5).
А Б В Г
(-6;-6;7) (16;-2;-3) (6;6;-7) (6;-2;-3)
4. Перпендикулярны ли векторы ⃗(2;3;6) и ⃗(3;2;−1).
А Б В
Да Нет Определить невозможно
5. Даны векторы ⃗(2;−1;4) и ⃗(5;3;). При каком значении х выполняется условие ⃗∙⃗=19?
А Б В Г
3 0 7/4 −(7/4)
6. Даны точки А(1;0;2), B(3;n;5), C(2,2,0), D(5,4,m). При каких значениях n и m векторы ⃗ и ⃗ – коллинеарны?
А Б В Г
=4/3;=9/2 =1/3;=2/3 =0,2;=0,5 Другой ответ
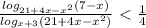
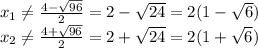
 ) U (
) U ( ; -2) U (-2;
; -2) U (-2;  ) U (
) U ( ; 7).
; 7).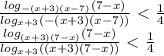
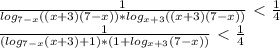
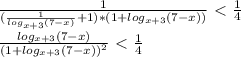
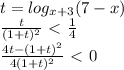
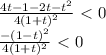
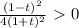
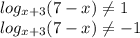
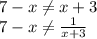
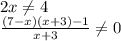
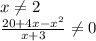
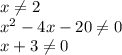
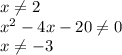
 ) U (
) U ( ; -2) U (-2; 2) U (2;
; -2) U (-2; 2) U (2;  ) U (
) U ( ; 7).
; 7).
ОДЗ: 21 + 4x - x² > 0
21 + 4x - x² ≠ 1
7 - x > 0
x + 3 > 0
x + 3 ≠ 1
21 + 4x - x² > 0
x² - 4x - 21 < 0
x² - 4x - 21 = 0
По теореме Виета: x₁ = -3, x₂ = 7.
x² - 4x - 21 < 0
x ∈ (-3; 7)
21 + 4x - x² ≠ 1
x² - 4x - 20 ≠ 0
D = 16 + 80 = 96
7 - x > 0
x < 7
x + 3 > 0
x > -3
x + 3 ≠ 1
x ≠ -2
Окончательно, ОДЗ: x ∈ (-3;
Решаем само неравенство:
Замена:
t ≠ 1
t ≠ -1
Делаем обратную замену:
Учитывая ОДЗ, окончательный ответ: x ∈ (-3;