Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через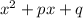
, другой - через 
.
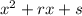Задача сводится к нахождению p, q, r, s. Тогда
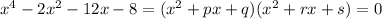
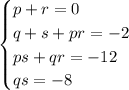
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
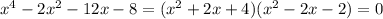
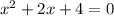не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).
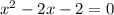
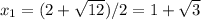
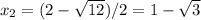
Сумма корней: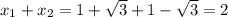 
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
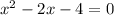
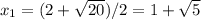
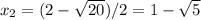
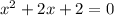не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).
Сумма корней: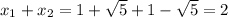 
ответ: 2.
ответ: со скорость 20 км/ч мотоциклист проедет весь путь.
Объяснение:
Пусть скорость велосипедиста х, тогда скорость мотоциклиста (х+10).
Время, за которое проезжает весь путь велосипедист 120/х, а мотоциклист 120/(х+10). Составим и решим уравнение:
120(х+10)-120х=6х(х+10)
120х+1200-120х=6х²+60х
6х²+60-1200=0 (разделим на 6)
х²+10+200=0
D=100-4*(-200)=900, √D=30
х1=(-10+30)/2=10 км/ч скорость велосипедиста
х2=(-10-30)/2=-20-не удовлетворяет условию задачи.
10+10=20 км/ч-скорость мотоциклиста.
ответ: со скорость 20 км/ч мотоциклист проедет весь путь.