Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
Для этого на примере рассмотрим графики функций у= , у=2 и у=
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.
Находим время, в течение которого поезда будут следовать друг мимо друга: t=(s₁+s₂)/(v₁+v₂)=(0,35км+0,42км)/(60км/ч+50км/ч)=0,007ч Находим искомое расстояние следующим образом: узнаем какое расстояние проехал поезд за время встречи 0,007ч и отнимем от этого расстояния длину поезда: Для первого поезда: l=v₁t-s₁=60км/ч·0,007ч-0,35км=0,07км=70м Для второго поезда: l=v₂t-s₂=50км/ч·0,007ч-0,42км=-0,07км=-70м Результаты получились противоположными, так как поезда едут в противоположных направлениях. В ответ идет модуль любого значения. ответ: 70 метров
Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a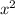
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
Для этого на примере рассмотрим графики функций у=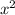 , у=2
, у=2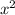 и у=
и у=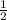
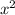
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.