Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
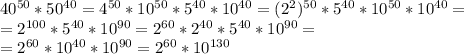
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
По условию их сумма равна 30.
Уравнение:
а+(а+d)+(a+2d)=30
a-2; a+d; a+2d - числа, составляющие геометрическую прогрессию
По свойству геометрической прогрессии
(a+d)²=(a-2)·(a+2d) - второе уравнение.
Решаем систему:
{а+(а+d)+(a+2d)=30
{(a+d)²=(a-2)·(a+2d)
Упрощаем каждое уравнение:
{a+d=10
{d²+4d+2a=0
Решаем систему подстановки
{a=10-d
{d²+4d+2·(10-d)=0
Решаем второе уравнение
d²+2d+20=0
дискриминант квадратного уравнения отрицателен.
Проверяйте условие