1. xn=2n-1;
n=1; x1=2*1-1=2-1=1;
n=2; x2=2*2-1=4-1=3;
n=3; x3=2*3-1=6-1=5;
n=4; x4=2*4-1=8-1=7;
n=5; x5=2*5-1=10-1=9.
***
2. xn=n²+1;
n=1; x1=1²+1=2;
n=2; x2=2²+1=5;
n=3; x3=3²+1=10;
n=4; x4=4²+1=17;
n=5; x5=5²+1=26.
***
3. xn=1/(n+1);
n=1; x1=1/(1+1)=1/2;
n=2; x2=1/(2+1)=1/3;
n=3; x3=1/(3+1)=1/4;
n=4; x4=1/(4+1)=1/5;
n=5; x5=1/(5+1)=1/6.
***
4. xn=(-1)^n;
n=1; x1=(-1)^1=-1;
n=2; x2=(-1)^2=1;
n=3; x3=(-1)^3=-1;
n=4; x4=(-1)^4=1;
n=5; x5=(-1)^5=-1.
Объяснение:
1. xn=2n-1;
n=1; x1=2*1-1=2-1=1;
n=2; x2=2*2-1=4-1=3;
n=3; x3=2*3-1=6-1=5;
n=4; x4=2*4-1=8-1=7;
n=5; x5=2*5-1=10-1=9.
***
2. xn=n²+1;
n=1; x1=1²+1=2;
n=2; x2=2²+1=5;
n=3; x3=3²+1=10;
n=4; x4=4²+1=17;
n=5; x5=5²+1=26.
***
3. xn=1/(n+1);
n=1; x1=1/(1+1)=1/2;
n=2; x2=1/(2+1)=1/3;
n=3; x3=1/(3+1)=1/4;
n=4; x4=1/(4+1)=1/5;
n=5; x5=1/(5+1)=1/6.
***
4. xn=(-1)^n;
n=1; x1=(-1)^1=-1;
n=2; x2=(-1)^2=1;
n=3; x3=(-1)^3=-1;
n=4; x4=(-1)^4=1;
n=5; x5=(-1)^5=-1.
ответ: 1.5 часа.
Объяснение:
учить все квадраты совсем нет необходимости... в редкой задаче встречаются квадраты чисел, больших 25
достаточно грамотно пользоваться формулами сокращенного умножения и приемами разложения на множители при вычислении дискриминанта и корни будут "извлекаться сами"...
ведь если уравнение квадратное,
то для решения или т.Виета (устно) или дискриминант))
за t обозначим время, которое нужно найти;
тогда путь S₂ = 27 км, время t,
скорость на этом участке пути v₂ = S₂/t = 27/t
путь S₁ = 67-27 = 40 км, время 4-t,
скорость на этом участке пути v₁ = S₁/t = 40/(4-t)
получили уравнение: 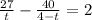
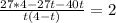
2t*(4-t) = 108-67t
2t² - 75t + 108 = 0
D = 75*75-4*2*108 = 9*25*25-8*4*27=9*(625-96)=(3*23)²
t₁ = (75+69)/4 = 144/4 > 4 часов--посторонний корень
t₂ = (75-69)/4 = 6/4 = 3/2 = 1.5