1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
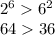
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
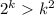
3) Тогда при n=k+1 должно выполняться неравенство:
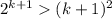
Вернемся к неравенству из второго пункта и домножим его на 2:
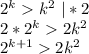
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
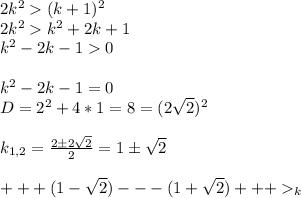
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если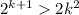 
, а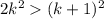 
, при k>5
То есть,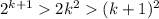 
, при k>5, то по закону транзитивности:
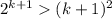, при k>5 - ч.т.д
1.
а)
б)
в)
г)
2. График на фото.
Область определения:
D(f)=(-∞;0)∪(0;+∞)
Функция принимает положительные значения при всех положительных Х, кроме 0(так как при нем знаменатель будет равен нулю).
3.
Получаем, что при всех значениях Y(кроме +-3) значение выражение будет равно 3, то есть какой бы Y мы не взяли, данное выражение всегда будет давать в ответе 3, что говорит о том, что оно не зависит от Y.
4.
Данное выражение имеет смысл при всех Х, кроме тех, при которых знаменатель будет равен 0.
x∈(-∞;0.8)∪(0.8;+∞)