Объяснение: y=f(x)
1) D(f) . Область определения - это множество значений "х", на котором задаётся функция . Если задан график, то, чтобы определить ООФ, надо все точки, лежащие на графике, спроектировать на ось ОХ. Полученное множество и будет ООФ.
Все точки данного графика проектируются на все точки оси ОХ. То есть получаем множество всех действительных чисел.
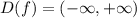
P.S. Множество значений функции E(f) - это значения, которые может принимать переменная "у" . Чтобы найти E(f) по графику, надо проектировать точки графика на ось ОУ. Для изображённой функции E(f)=[ -2; 2 ] .
2) Точка пересечения с осью ОХ - (0,0). Эта же точка (0,0)- точка пересечения с осью ОУ.
3) Функция возрастает на промежутке [ -3; 3 ] , х∈[ -3;3 ]. Если вести карандашом по графику от точки (-3,-2) до точки (3,2), то карандаш движется вверх, функция возрастает.
Промежутков убывания нет (нет участков, на которых карандаш движется вниз) .
P.S. Есть промежутки постоянства функции (где карандаш движется по прямой), это участки х∈(-∞ -3] и х∈[ 3,+∞).
4) Нули функции - это значения "х", при которых "у" обращается в 0 . Для изображённой функции - это х=0 (см. пункт 2). То есть f(0)=0.
5) Наибольшее значение функции - это у=2 , наименьшее значение функции - это у= -2 ( cм. пункт 1 , P.S. )
Парабола у=х²,ветви вверх,вершина (-1;-1),точки пересечения с осями (-3;0),(-1;0),(0;3)
а)(-2;∞)
б)(-∞;-2)
в)наиб нет
наим у=-1
г)(-3;-1)
2)Это парабола у=(х-1)²-9, ветви вверх,вершина (1;-9),точки пересечения с осями (-2;0),(4;0),(0;-8)
3)у=4/х гипербола в 1 и 3ч
х -4 -2 -1 1 2 4
у -1 -2 -4 4 2 1
у=/х+1/-4
х -5 -4 -3 -2 -1 0 1 2 3 4
у 0 -1 -2 -3 -4 -3 -2 -1 0 1
ответ (-4;-1);(-2;-4),(4;1)