 — общее число человек на экзамене по математике.
— общее число человек на экзамене по математике. ,
,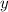 . Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается:
. Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается: 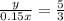 , отсюда
, отсюда 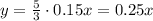 .
. , решили с ошибками 144, решили правильно
, решили с ошибками 144, решили правильно 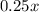 . Вместе эти три группы есть общее число человек на экзамене, то есть
. Вместе эти три группы есть общее число человек на экзамене, то есть  . Получаем:
. Получаем: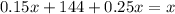
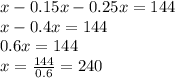
750 чисел
Объяснение:
На 2 делятся чётные числа, поэтому на месте числа единиц числа может стоять цифра 0, 2, 4 и 6.
1) Число единиц равно выбора
На остальные места тысяч, сотен, десятков и единиц выбираем числа из данных: 1,2,3,4,5,6,7 (всего 7 цифр).
Тысячи выбора, сотни десятки
Перемножим полученное количество чисел.
2) Число единиц равно выбора
На остальные места тысяч, сотен, десятков и единиц выбираем числа из данных: 0,1,3,4,5,6,7 (всего 7 цифр). Но, ноль нельзя поставить на место тысяч!
Тысячи - 6, сотни - 6, десятки - 5
Перемножим полученное количество
3) Аналогичные результаты (см. 2) получим, если поставим на место единиц цифры 4 и 6.
4) Осталось сложить все полученные результаты:
210+3*180=210+540=750 четырёхзначных чисел можно составить