Записать диагональное отношение во множестве А⊕В, если
А = {a, b, (c, d), e, f}, B = {c, d, e, g, {f}}.
2. Во множестве А = {1, 2, 3, 4, 5, 6, 7, 8, 9} задано отношение R так: "элемент а находится в отношении с элементом b, если a и b имеют одинаковое количество натуральных делителей. Если количество натуральных делителей обозначить через k, то
R={|k(a)=k(b), a,b є A}
1) доказать, что R - отношение эквивалентности;
2) выписать все классы эквивалентности по отношению R;
3) записать множество А через объединение различных классов эквивалентности;
4) записать фактор-множество по отношению эквивалентности R.
2. Заполнить таблицу
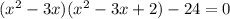
x² + 2x - 3 = 0
По теореме Виета:
x₁ = -3
x₂ = 1
f'(x) > 0, x ∈ (-∞; -3) и f'(x) < 0, x ∈ (-3; -1) U (-1; 1) ⇒ x₁ = -3 -- точка локального максимума
f'(x) < 0, x ∈ (-3; -1) U (-1; 1) и f'(x) > 0, x ∈ (1; +∞) ⇒ x₂ = 1 -- точка локального минимума
2.
Непрерывная на отрезке функция может достигать своего наибольшего и наименьшего значений лишь на концах отрезка и в точках экстремума.
x = 6 ∉ [0; 3] ⇒ функция достигает своего наибольшего и наименьшего значений на концах отрезка.
x = 0 -- точка максимума
x = 3 -- точка минимума
Подробнее - на -