Возведём обе части в квадрат:
(√(2x-20) + √(x+15))² = 25
Теперь всё раскрываем:
2x - 20 + 2√((2x-20)(x+15)) + x + 15 = 25
Теперь всё кроме корня перенесём вправо с противоположным знаком и вновь возведём в квадрат:
2√((2x-20)(x+15)) = 30 - 3x
4√((2x-20)(x+15))² = (30 - 3x)²
4(2x-20)(x+15) = (30 - 3x)²
4(2x² + 30x - 20x - 300) = 900 - 180x + 9x²
8x² + 120x - 80x - 1200 = 900 - 180x + 9x²
-x² + 220x - 2100 = 0
x² - 220x + 2100 = 0
x1 = 210; x2 = 10
Теперь попытаемся подставнокой проверить, какой корень будет удовлетворять уравнению:
ответ: 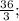 ∞
∞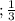
Объяснение:
a)
В этом задании требуется найти определенный интеграл на отрезке x ∈ (1,3). Находим первообразную:
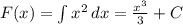
Подставляем в нее границы интегрирования, чтобы найти определенный интеграл:
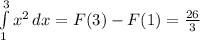
б)
Тоже самое что и в задании а). Находим первообразную функции:
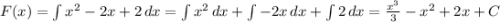
Подставляем в первообразную границы интегрирования. Они определяются через пресечение параболой оси OY:
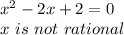
Мы получили, что нет таких точек, которые бы удовлетворяли уравнению, а значит, нет пересечения с OY и площадь ⇒∞.
в)
Находим первообразные для каждой из написанных функций:
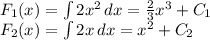
Теперь находим пересечение двух графиков функций. Это и будут границы интегрирования:
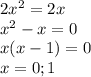
Находим площади под каждой из двух функций при определенного интеграла:
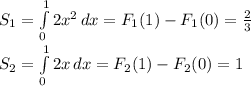
Теперь, чтобы найти общую площадь фигуры вычитаем из большей площади меньшую:
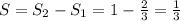
Решение системы уравнений х=18,75
у=15
Объяснение:
Решить систему уравнений методом подстановки.
(x+y)/15−(x−y)/3=1
(2x−y)/6−(3x+2y)/3=−25
Умножим первое уравнение на 15, а второе на 6, чтобы избавиться от дробного выражения:
x+y-5(x−y)=15
2x−y-2(3x+2y)= -150
Раскрываем скобки:
х+у-5х+5у=15
2х-у-6х-4у= -150
Приводим подобные члены:
6у-4х=15
-5у-4х= -150
Разделим второе уравнение на -5 для удобства вычислений:
6у-4х=15
у+0,8х=30
Выразим у во втором уравнении через х, подставим выражение в первое уравнение и вычислим х:
у=30-0,8х
6(30-0,8х)-4х=15
180-4,8х-4х=15
-8,8х=15-180
-8,8х= -165
х= -165/-8,8
х=18,75
Теперь значение х подставляем в любое из двух уравнений системы и вычисляем у:
6у-4х=15
6у=15+4*18,75
6у=90
у-90/6
у=15
Решение системы уравнений х=18,75
у=15