1) найдём произведение всех чисел в квадрате: так как произведение чисел в одной строке отрицательно, то произведение всех чисел (5 строк) будет отрицательно. Но с другой стороны, произведение всех чисел равно и произведению чисел в столбцах (5 столбцов). А так как произведение всех чисел отрицательно, то найдется столбец, в котором произведение чисел является отрицательным. 2) Произведение четного и четного числа-число четное, поэтому после стирания четного числа-четное число останется на доске. Произведения нечетного числа на 9 оканчивается цифрой 9, поэтому после стирания 9 и нечетного числа, мы ее снова записываем на каком-то этапе сотрет четное число и цифру 5, тогда на доске появится 1, который "обнулит" все другие цифры на каком-то этапе итого 9 -последняя цифра значит ответ
а) 2x^2-11x+12=0
2x^2-3x-8x+12=0
(2x-3)*(x-4)=0
2x-3=0 или x-4=0
2x=0+3 x=4
2x=3
x=3:2
x=1,5
б) 14x^2=9x
14x^2-9x=0
x(14x-9)=0
x=0 или 14x-9=0
x=9/14
в) 16x^2-49=0
16x^2=49
x^2=49:16
x^2=49/16
x=±7/4
г) x^2-36x+323=0
x(x-17)-19(x-17)=0
(x-17)(x-19)=0
x-17=0 или x-19=0
x=17 x=19
2.
p=46=2(a+b) все это делим на 2 чтобы от нее избавиться
23=a+b
b=23-a
s=120=ab
120=a(23-a)
120=23a-a^2
-a^2+23a-120=0
d=23^2-480=529-480=49
x1=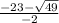 = -23-7/-2=-30/-2=15
= -23-7/-2=-30/-2=15
x2=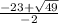 =-23+7/-2=-16/-2=8
=-23+7/-2=-16/-2=8
3.x^2+px=36=0 (a=1; b=p; c=36)
d=p^2-144
12=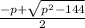
p=-15
x2=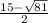 =15-9/2=6/2=3
=15-9/2=6/2=3