По формуле классической вероятности: p=m/n n=90 ( количество двузначных чисел)
Числа делящиеся на 3: 12; 15;... 99 - таких чисел 30 Можно найти их количество по формуле n-го члена арифметической прогрессии a₁=12 d=15-12=3 99=12+3·(n-1) ⇒87=3(n-1) n-1=29 n=30
Числа делящиеся на 5: 10; 15;20; 25; 30;...; 95 - таких чисел 30 Можно найти их количество по формуле n-го члена арифметической прогрессии a₁=10 d=15-10=5 95=10+5·(n-1) ⇒85=5(n-1) n-1=19 n=20
Чисел, которые одновременно делятся и на 3 и на 5 всего 6: 15;30;45;60;75 и 90
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)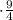 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит,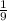 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда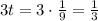 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно,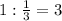 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.