Доказательство:
1. Пусть студентов-участников лагеря было х человек, а вес всей приготовленной пищи равен у г.
Тем, кто слушал лекции, выдали во время обеда
0,25•у г. Каждому слушателю досталась порция в 0,25у : (х/3) = у/4 : х/3 = у/4•3/х = (3у)/(4х) г.
2. Тем, кто поехал на экскурсию, а их 2х/3 человек, выдали порции, вес которых
1,5•(3у)/(4х) = 4,5у/(4х) = 9у/(8х).
Вес всех этих порций равен
(2х)/3•(9у)/(8х) = (2х•9у)/ (3•8х) = (1•3у)/ (1•4) = (3у)/4 г.
3. Всем студентам вместе выдали
0,25у + (3у)/4 = 0,25у + 0,75у = у (граммов) - вес всей приготовленной пищи.
Вывод: дети съели всю приготовленную еду.
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.

1. 1) Очевидно
2) Очевидно
3) Очевидно ибо под учеником подразумевается 12 девочек и 13 мальчиков, т.е. всего учеников 12 + 13 = 25.
4) К любой из 12 девочек в пару можно взять любого из 13 мальчиков. По правилу произведения всего существует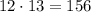 выбрать мальчика с девочкой.
выбрать мальчика с девочкой.
ОТВЕТ: 1) 12; 2) 13; 3) 25; 4) 156.
2. Есть 10 цифр, из которых нужно составить четырехзначные числа.
1) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0, т.е. существует выбрать цифру, обозначающую тысячи. На втором месте может стоять любая из 9 оставшихся цифр, т.е. цифру, обозначающую сотни, также можно выбрать Аналогично цифру, обозначающую десятки, можно выбрать так как останется 8 цифр; цифру, обозначающую единицы
По правилу произведения всего можно составить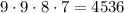 четырехзначных чисел.
четырехзначных чисел.
2) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0 - имеем выбора первой цифры. Однако так как цифры могут повторяться, каждую следующую цифру числа можно выбрать
По правилу произведения всего можно составить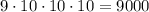 четырехзначных чисел.
четырехзначных чисел.
ОТВЕТ: 1) 4536; 2)9000.