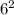Реши квадратное уравнение 2(4x−14)^2−10(4x−14)+8=0 (первым вводи больший корень): x1 = x2 = Дополнительный во какой метод рациональнее использовать? Метод введения новой переменной Раскрытие скобок Вынесение за скобку Разложение на множители
Уравнение прямой на плоскости имеет в общем случае (когда прямая не параллельна ни одной из координатных осей) вид ax+by+c=0, где x и y - координаты любой точки, принадлежащей прямой. 1) При a=0 уравнение прямой принимает вид by+c=0, или y=-c/b. Это значит, что все точки нашей прямой имеют одинаковую ординату y=-c/b, а это означает, что прямая параллельна прямой Ox. 2) При b=0 уравнение принимает вид ax+c=0, или x=-c/a. Это значит, что все точки прямой имеют одинаковую абсциссу x=-c/a, т.е. прямая параллельна оси Oy. По условию, a=5, c=5, и уравнение принимает вид x=-5/5=-1. ответ: уравнение прямой есть х=-1
Объяснение:
Метод введения новой переменной:
2(4x−14)^2−10(4x−14)+8=0
4x−14 = у
2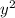 -10y+8=0
-10y+8=0
D = - 4 * 2 * 8 = 36 =
- 4 * 2 * 8 = 36 =