у>0 на интервале (-∞;2-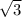 
) и (2+ ;+∞)
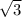у<0 на интервале (2- 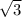; 2+ )
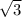Объяснение:
1) Находим область определения функции.
Это квадратичная функция. График - парабола
Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Находим нули функции.
Чтобы найти нули функции нужно решить уравнение x²-4x+1=0, то есть найти те значения «икс», при которых функция обращается в ноль.
x²-4x+1 = 0
х₁ = 2- 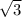, х₂ = 2-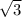
3) Откладываем все найденные точки на числовой оси:
___..___
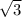2- 2+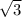
В данном случае ветви параболы направлены вверх (т.к. коэффициент при х² больше 0), следовательно, на интервалах (-∞;2- 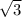) и (2+ ;+∞)
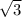функция будет положительна, а на интервале 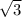(2- ; 2+ 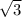) - функция будет отрицательна.
Расстояние по течению = 112 км
расстояние против течения = 112 км
Находим скорость по течению: (11 + x)
находим скорость против течения: ( 11 - x)
Теперь надо найти время:
время по течению : 112 / (11 + x)
время против течения : 112/( 11 - x)
В условии сказано,что на обратный путь затрачено на 6 часов меньше.Чем больше скорость,тем меньше времени.Составим уравнение:
112/( 11- x) - 112/(11 + x) = 6
(1232 + 112x - 1232 + 112x) / ( 11-x)( 11 + x) = 6
224x / ( 121 - x²) = 6
726 - 6x² = 224x
- 6x² - 224x + 726 = 0
3x² + 112x - 363 = 0
D = b² - 4ac = 12544 + 4356 = 16900 = 130²
x1 = ( - 112 + 130) / 6 = 3
x2 = ( - 112 - 130 ) / 6 ≈ - 40,3 - меньше 0 - не имеет решения к задаче,значит,
скорость течения равна 3 км/ч.
ответ: 3 км/ч.