Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 45 см
Объяснение:
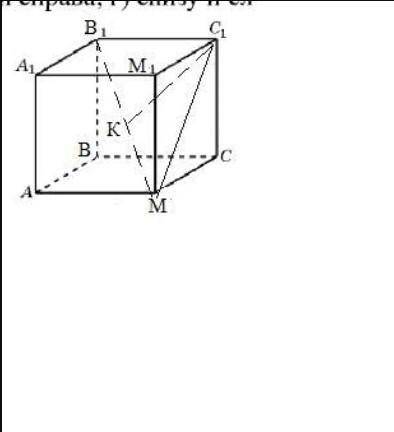
Пусть АВСМА₁В₁С₁М₁-куб, АВ=45см. Все грани равные квадраты.Расстоянием от вершины С₁ до диагонали В₁М будет длина перпендикуляра С₁К.
Найдем диагональ квадрата по т. Пифагора ⇒ 45√2 см.
Найдем диагональ куба d²=45²+45²+45² , d²=3*45² , d=45√3 см.
ΔМВ₁С₁- прямоугольный, т.к. проекция М₁С₁⊥ В₁С₁ , то и наклонная МС₁⊥В₁С₁ по т. о трех перпендикулярах. Используя формулу площади треугольника :
S(В₁С₁М)=1/2*В₁С₁*С₁М или S(В₁С₁М)=1/2*В₁М*С₁К ⇒
S(В₁С₁М)=1/2*45*45√2 , подставим во вторую формулу, получим :
1/2*45*45√2=1/2*45√3*С₁К или С₁К=(45√2)/√3=(45√6)/3=15√6 (см)
В решении.
Объяснение:
Побудуйте графік функції у = 3(х – 2)2 за до геометричних перетворень. Підготуйте таблицю значень початкової функції у = х2, вибравши зручні для побудови значення аргументу.
Постройте график функции у = 3(х – 2)² с геометрических преобразований. Подготовьте таблицу значений начальной функции
у = х², выбрав удобные для построения значения аргумента.
График функции у = 3(х – 2)² парабола, получен при сдвиге классической параболы у = х² на две единицы вправо и "уже" её за счёт множителя 3.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х 0 1 2 3 4
у 12 3 0 3 12
По вычисленным точкам построить параболу.
Таблица значений начальной функции у = х²:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9