Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²= 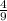
ответ: 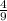
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a= 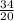
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с= 
с= 
совокупность:
с= 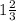
с= 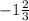
у = х -8;
ху = -7.
Подставляем у = х -8 во второе уравнения и находим х:
х (х-8) = -7;
х^2 -8x -7 =0
В результате получаем квадратное уравнение. Ищем дискриминант:
D= b^2-4ac = (-8)^2 -4*1*(-7) = 64+28=92;
х1= (-b-√D)/2a = (8-√92)/2 = (8 - 4√23)/2 = 2(4 -2√23)/2 = 4 -2√23;
х2= (-b+√D)/2a = (8+√92)/2 = (8 + 4√23)/2 = 2(4 +2√23)/2 = 4 +2√23;
Вспоминаем про наше первое уравнение и находим у = х -8:
у1 = 4 -2√23 -8 = -4 -2√23 =-2(2+√23);
у2 = 4 +2√23 -8 = -4 +2√23 =-2(2- √23).
ответ: (4 -2√23; -2(2+√23)); (4 +2√23; -2(2- √23).
sin