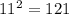. Далее откидываем от вновь получившегося числа ещё одну цифру(то есть стремимся, чтоб число состояло из двух цифр, ибо нужно узнать две последние цифры), получаем 21. 
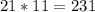. Проделываем ту же операцию ещё несколько раз: 
... Наблюдаем закономерность: который раз мы умножаем получившееся число на 11, такая цифра и будет второй с конца(2011 * 2011 = ...21; ...21 * 2011 = ...31; ...31 * 2011 = ...41; и т.д., притом после накрутки первого десятка вторая цифра онулируется и всё по новой...), а первая с конца всегда единица. Таким образом, 
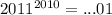, а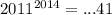 
.
1.в
2.в
3.в
4.б
5.б
6.а
7.а) x1=0; x2=6; б) x1=-0,4; x2=0,4;
8.(2x+9)*(x-1)=0
x1= -4.5; x2= 1;
9. x^2-5x+4
10. (3x+1)^2=4x^2+5x-1
5x^2+5x+2=0
дискриминант отрицательный.
11. x1=-4; x2=-3; x3=3; x4=4;
12. За т. Вієта сума коренів квадратного рівняння дорівнює другому коефіцієнтові, взятому із протилежним знаком (тобто, x_1+x_2=14)
Формулу x_1^2+x_2^2 можна представити як (x_1+x_2)^2-2x_1*x_2, але для цього ми маємо знати ще добуток коренів.
Добуток коренів (знову-таки за т. Вієта) дорівнює третьому коефіцієнтові (тобто, x_1*x_2=5)
Підставимо значення у формулу: (x_1+x_2)^2-2*x_1*x_2=14^2-2*5=196-10=186