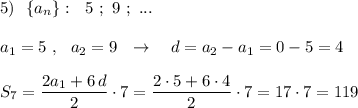

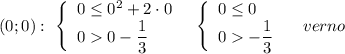
Для других точек хотя бы одно неравенство будет неверным.
Например,
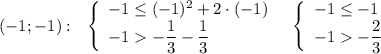 неверно 2 неравенство
неверно 2 неравенство
7) Из города А в город В ведут 8 дорог. Обозначим их: 1,2,3,4,5,6,7,8 .
Из города В в город С ведут 9 дорог. Обозначим их: a,b,c,d,e,f,g,i,k .
Тогда можно написать, какие маршруты могут быть.
(1,a) (1,b) (1,c) (1,d) (1,e) (1,f) (1,g) (1,i) (1,k)
(2,a) (2,b) .......................................................... (2,k)
(3,a) (3,b)............................................................. (3,k)
........................................................................................
(8,a) (8,b).............................................................. (8,k)
Образовалась таблица из 8 строчек и 9 столбцов. Количество элементов в этой таблице равно 8*9=72 . Поэтому и маршрутов может быть 72 .
-3
Объяснение:
Хорошо, что дали картинку, потому что текстом вы написали полную кашу, в которой ничего непонятно.
(7x+3y)/(x+5y) + (3x-2y)/(2x+y) = 4
Можно попробовать выразить y через x.
Умножим все на (x+5y)(2x+y) и избавимся от дробей.
(7x+3y)(2x+y) + (3x-2y)(x+5y) = 4(x+5y)(2x+y)
14x^2 + 6xy + 7xy + 3y^2 + 3x^2 - 2xy + 15xy - 10y^2 = 8x^2 + 40xy + 4xy + 20y^2
Приводим подобные и собираем все в левой части:
(17-8)x^2 + (13+13-44)xy + (-7-20)y^2 = 0
9x^2 - 18xy - 27y^2 = 0
Делим всё на 9
x^2 - 2xy - 3y^2 = 0
Делим всё на y^2
(x/y)^2 - 2(x/y) - 3 = 0
Обозначим x/y = n
n^2 - 2n - 3 = 0
(n+1)(n-3) = 0
1) n = x/y = -1; x = -y; x^2 = y^2, тогда:
t = (x^2 + 2y^2)/(x^2 - 2y^2) = 3y^2/(-y^2) = -3
2) n = x/y = 3; x = 3y; x^2 = 9y^2, тогда:
t = (x^2 + 2y^2)/(x^2 - 2y^2) = 11y^2/(7y^2) = 11/7
Наименьшее из чисел (-3; 11/7) = -3