1.(x,y)=(10,5) 2.(x,y)=( -1, -2) 3.(x,y)=( -5,0) 4.(x,y)=(5,1)
Объяснение:
1.
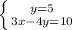1.2(3+2y)+y=-4 1.-5+y-3y=-5 1.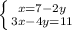
2.3x-4*5=10 2.y=-2 2.y=0 2.3(7-2y)-4y=11
3.x=10 3.x=3+2(-2) 3.x=-5+0 3.y=1
4.x=-1 4.x=-5 4.x=7-2*1
5.x=5
ответ: S=1/3 кв. ед.
Объяснение:
f(x)=x²-4x x₀=1 x=0 S=?
yk=y(x₀)+y'(x₀)*(x-x₀)
y(1)=1²-4*1=1-4=-3.
y'(1)=(x²-4x)'=2x-4=2*1-4=2-4=-2. ⇒
yk=-3-2*(x-1)=-3-2x+2=-2x-1.
y=x²-4x y=-2x-1 x=0 S=?
x²-4x=-2x-1
x²-2x+1=0
(x-1)²=0
x-1=0
x=1. ⇒
S=₀∫¹(x²-4x-(-2x-1)dx=₀∫¹(x²-4x+2x+1)dx=₀∫¹(x²-2x+1)dx=
=₀∫¹x²dx-₀∫¹2xdx+₀∫¹dx=(x³/3-x²+x) ₀|¹=(1³/3)-1²+1-(0³/3-0²+0)=1/3.