Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
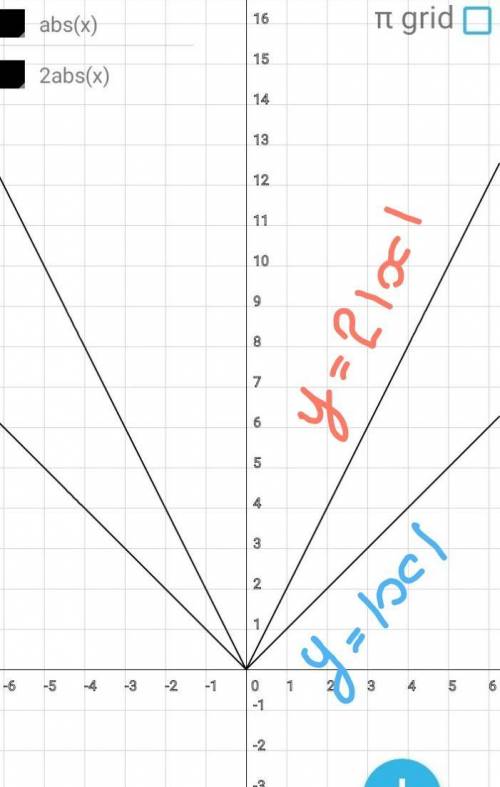
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
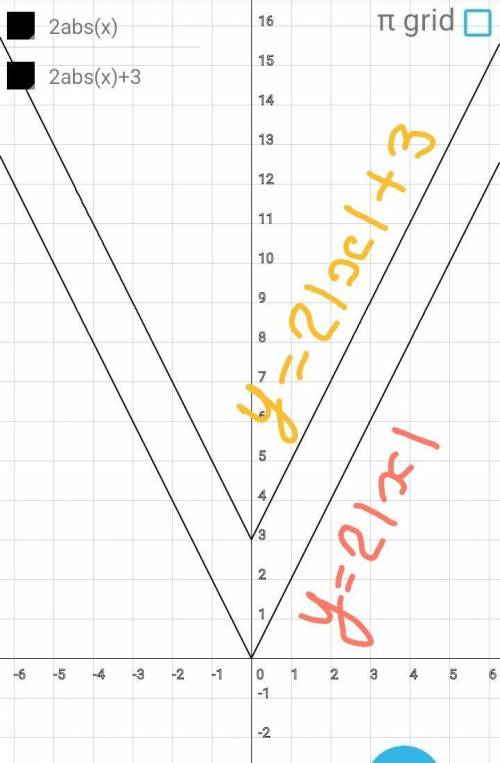
Шаг 3.
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
z1+z2=(10-8)+(-4+1)i=2-3i
z1-z2=(10+8)+(-4-1)i=18-5i
z1*z2=(10-4i)*(-8+i)=-80+32i+10i-4i^2=(80+4)+(32+10)i=84+42i
Объяснение:
вроде бы так..