Пояснення: Например, есть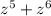 
. Мы выносим то, что есть общее. Здесь общее 
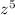, из-за этого у нас получается z^5(1+z). При умножении степени не умножаются, а прибавляются. Если мы будем множить обратно, получается:
z(1+z) = z^5 * 1 + z^5 * z = z^5 + z^6
Объяснение:
Выносим общий множитель √2*sinx за скобки
√2*sinx*(2-cosx)+cosx-2=0
Выносим знак минус за скобку
√2*sinx*(2-cosx)-(2-cosx)=0
Выносим за скобку общий множитель 2-cosx
(2-cosx)*(√2*sinx-1)=0
2-cosx=0 или √2*sinx-1=0
1) -cosx=-2 - не существует, поскольку cosx принадлежит [-1:1]
2) √2*sinx=1 делим на √2
sinx= 1/√2
sinx= 1/√2
используем обратную тригонометрическую ф-цию
x=arcsin(1/√2)
sinx периодическая ф-ция добавляем 2Пn, n принадлежит Z
x=arcsin(1/√2)+2Пn, n принадлежит Z
Решаем уравнение
x=п/4+2Пn, n принадлежит Z
Вроде так
1 + z получилось, т.к. общий множитель z4 (четыре z и пять z, общий четыре, поэтому остаётся 1 и z, если перемножить то получиться первоначальный вид z4 + z5)