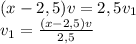
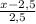 раза выше. Приравняем теперь полное расстояние между пунктами А и В. Время в пути для велосипедиста Х, для мотоциклиста Х-12, скорость велосипедиста v, скорость мотоциклиста -
раза выше. Приравняем теперь полное расстояние между пунктами А и В. Время в пути для велосипедиста Х, для мотоциклиста Х-12, скорость велосипедиста v, скорость мотоциклиста - 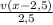 , S=t*v.
, S=t*v.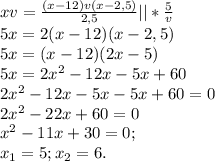
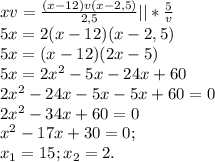
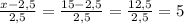 раз выше скорости велосипедиста. Следовательно, на дорогу ему нужно впятеро меньше времени. 15/5=3, 15-12=3. ответ верен.
раз выше скорости велосипедиста. Следовательно, на дорогу ему нужно впятеро меньше времени. 15/5=3, 15-12=3. ответ верен.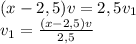
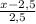 раза выше. Приравняем теперь полное расстояние между пунктами А и В. Время в пути для велосипедиста Х, для мотоциклиста Х-12, скорость велосипедиста v, скорость мотоциклиста -
раза выше. Приравняем теперь полное расстояние между пунктами А и В. Время в пути для велосипедиста Х, для мотоциклиста Х-12, скорость велосипедиста v, скорость мотоциклиста - 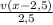 , S=t*v.
, S=t*v.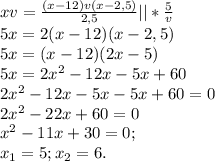
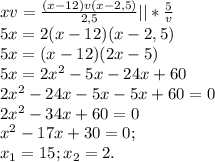
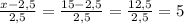 раз выше скорости велосипедиста. Следовательно, на дорогу ему нужно впятеро меньше времени. 15/5=3, 15-12=3. ответ верен.
раз выше скорости велосипедиста. Следовательно, на дорогу ему нужно впятеро меньше времени. 15/5=3, 15-12=3. ответ верен.
ответ: x∈(-∞;+∞).
Объяснение:
Так как (х-5)²≥0, ⇒ (х-5)²+1>0
x∈(-∞;+∞).