ОДЗ:
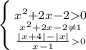
Решаем каждое неравенство:
 ⇒
⇒ 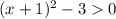 ⇒
⇒

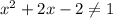 ⇒
⇒  ⇒
⇒ 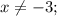
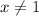

Подмодульные выражения обращаются в 0 в точках
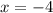 и
и 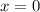
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
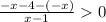 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
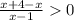 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 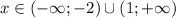
ОДЗ:

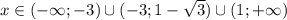
Решаем неравенство: 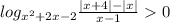
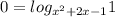
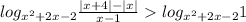
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
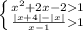 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
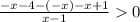 ⇒
⇒  ⇒
⇒ 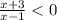 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
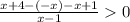 ⇒
⇒ 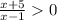 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 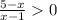 ⇒
⇒ 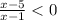 ⇒
⇒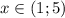
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
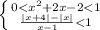 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
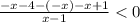 ⇒
⇒ 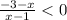 ⇒
⇒ 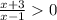 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
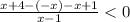 ⇒
⇒ 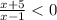 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 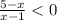 ⇒
⇒ 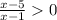 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: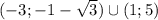
Подробное объяснение:
1) Ищем нули функции:
первая скобка равна нулю при х=-2
вторая скобка равна нулю при х=4
2) Рисуем числовую ось и расставляем на ней найденные нули
функции - точки -2 и 4
(-2)(4)
Точки рисуем с пустыми кружочками ("выколотые"), т.к.
неравенство у нас строгое (знак < )
3) Начинаем считать знаки на каждом интервале, начиная
слева-направо. Для этого берём любую удобную для подсчёта
точку из интервала, подставляем её вместо икс и считаем знак:
1. х=-100 -100+2 <0 знак минус
-100-4 <0 знак минус
минус*минус=плюс
Ставим знак плюс в крайний левый интервал
+
(-2)(4)
2. аналогично,
х=0 0+2 >0 знак плюс
0-4 <0 знак минус
плюс*минус=минус
+ _
(-2)(4)
3. x=100 100+2>0 знак плюс
100-4>0 знак плюс
плюс*плюс=плюс
+ - +
(-2)(4)
Итак, знаки на интервалах мы расставили.
Смотрим на знак неравенства: < 0 Значит, нам надо взять
только те интервалы, где стоят минусы.
В данном случае, такой интервал один (-2;4)
Это и есть ответ.
Теперь краткая запись решения:
(х+2)(х-4)<0
+ - +
(-2)(4)
x∈(-2;4)
ответ: (-2;4)