3. Функция задана формулой y=-2x+4
a) Найдите область определения
b) Найдите координаты точки пересечения графика функции с осью абсцисс
c) Возрастающей или убывающей является функция
ОЧЕНЬ

👇

Увидеть ответ

Открыть все ответы

Ответ:

ApokalipsisZnanij

17.09.2020

x = п/8 + пn/2

Перебираем все целые числа n

если n=0, то x= п/8 (корень подходит)

если n=1, то x= 5п/8 (корень подходит)

если n=2, то x= 9п/8 (корень не подходит, потому что больше п), следовательно, все n, которые больше 2, не будут удовлетворять условию. Переходим на отрицательные.

если n=-1, то x= -3п/8 (корень подходит)

если n=-2, то x= -7п/8 (корень подходит)

если n=-3, то x= -11п/8 (корень не подходит, потому что меньше -п), следовательно, все n, которые меньше -3, не будут удовлетворять условию.

х = -п/4 + пn/2

Перебираем все целые числа n

если n=0, то x= -п/4 (корень подходит)

если n=1, то x= п/4 (корень подходит)

если n=2, то x= 3п/4 (корень подходит)

если n=3, то х= 5п/4 (корень не подходит, потому что больше п), следовательно, все n, которые больше 3, не будут удовлетворять условию. Переходим на отрицательные.

если n=-1, то x= -3п/4 (корень подходит)

если n=-2, то x= -5п/4 (корень не подходит, потому что меньше -п), следовательно, все n, которые меньше -2, не будут удовлетворять условию.

4,5(83 оценок)

Ответ:

Fanny321

17.09.2020

Находим производную:

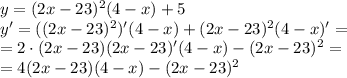
$y=(2x-23)^{2}(4-x)+5\\ y'= ((2x-23)^{2})'(4-x)+(2x-23)^{2}(4-x)'=\\=2 \cdot (2x-23)(2x-23)'(4-x) -(2x-23)^{2}= \\ =4(2x-23)(4-x)-(2x-23)^{2}$

Упростим.

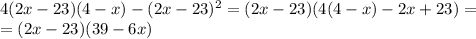
$4(2x-23)(4-x)-(2x-23)^{2}= (2x-23)(4(4-x)-2x+23)=\\= (2x-23)(39-6x)$

Найдем периоды возрастания и убывания:

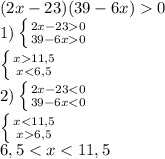
$(2x-23)(39-6x)0\\ 1) \left \{ {{2x-230} \atop {39-6x0}} \right.\\ \left \{ {{x11,5} \atop {x<6,5}} \right.\\ 2) \left \{ {{2x-23<0} \atop {39-6x<0}} \right.\\ \left \{ {{x<11,5} \atop {x6,5}} \right.\\ 6,5<x<11,5$

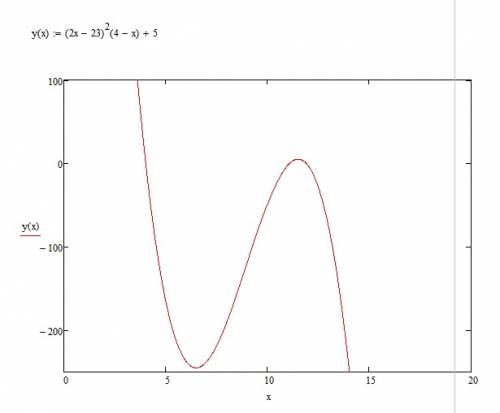
На промежутке от 6,5 до 11,5 функция возрастает, на остальном она убывает. Имеем две точки экстремума:

6,5 - точка минимума

11,5 - точка максимума.

У нас пулучается, что функция примет свое наименьшее значение в точке минимума, то есть в точке 6,5. Подставляем в функцию:

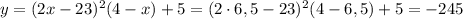
$y=(2x-23)^{2}(4-x)+5 = (2\cdot 6,5-23)^{2}(4-6,5)+5 = -245$

График для наглядности.

З.Ы. Здесь небольшой подвох есть. В точке х =14, у тоже будет равен -245. Поскольку, в рассматриваемом промежутке [0; 14), точка 14 не включена, то тогда мы не берем ее в расмотрение.