a) x-8≥2(x+½)+7
x-8≥2x+1+7
x-8≥2x+8
x-2x≥8+8
-x≥16
x≤-16
b) x(x+3)>(x+1)(x+3)
x²+3x>x²+4x+3
x²+3x-x²-4x>3
-x>3
x<-3
c) (3x-1)/5-(x+1)/2<1-x/7
2(3x-1)/10-5(x+1)/10<1-x/7
(6x-2-5x-5)/10<7/7-x/7
(x-7)/10<(7-x)/7
(70*(x-7))/10<(70*(7-x))/7
7*(x-7)<10*(7-x)
7x-49<70-10x
7x+10x<70+49
17x<119
x<119/17
x<7
d) (9x+2)/10-(10x-2)/9>2
(9*(9x+2)-10*(10x-2))/90>2
(81x+18-100x+20)/90>2
(-19x+38)/90>2
(90*(-19x+38))/90>2*90
-19x+38>180
-19x>180-38
-19x>-142
x<-142/19
x<-7 9/19
f(x) = 1/3 x^3 - x^2 + 6
Продифференциируем функцию
f ' (x) = x^2 - 2x
Приравняем производную к нулю
x^2 - 2x = 0
x (x - 2) = 0
x = 0, или x - 2 = 0
Из вышеназванного следует, что точки экстремума - это ноль и два
Возьмём число один, для проверки знаков в следующих промежутках
(минус бесконечность ; ноль), (ноль ; два), (два ; плюс бесконечность)
f ' (1) = 1 - 2 = - 1
Значит, что в среднем промежутке будет знак минус, в боковых плюс, из чего следует, что на промежутке от минус бесконечности до нуля производная функции положительна (сама функция возрастает), на промежутке от нуля до двух производная отрицательна (функция убывает), а на промежутке от двух до плюс бесконечности производная опять становится положительной, а функция возрастает...
Точка "ноль" - точка максимума
Точка "два" - точка минимума
Фатимка, дальше я не знаю, как решать, но надеюсь, что материал вам пригодится
и 
. Чтобы найти для них общий знаменатель, нужно найти найменьшее общее число которое нацело делилось бы на знаменатель первого и второго дроба, в даном случае знаменатели это 25 и 4. Ну можно взять больший знаменатель умножить на 2 и проверить делится ли это число нацело на первый и другой знаменатель, если не делится ужножаеш на 3 и проверяеш, и так далее. Часто бывает, что один с знаменателей уже делится на себя и на второй знаменатель, тогда это и будет общий знаменатель. Потом оно само будет получаться, потому что будешь знать что на что делится.+ ;
;
= 
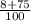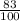, если можно сократить (то есть и числитель и множитель делится на одинаковое число), то сокращаем.
Объяснение:
a) x-8>>2x+1+7, -x>>16, x<<-16, отв -16
b) x^2+3x>x^2+4x+3, -x>3, x<-3, отв. -4
с)умножаем все на 70 и сокращаем,
14(3x-1)-35(x+1)<70-10x, 42x-14-35x-35<70-10x,
17x<119, x<7 (7), отв 6