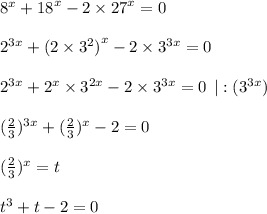
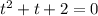
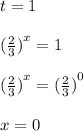

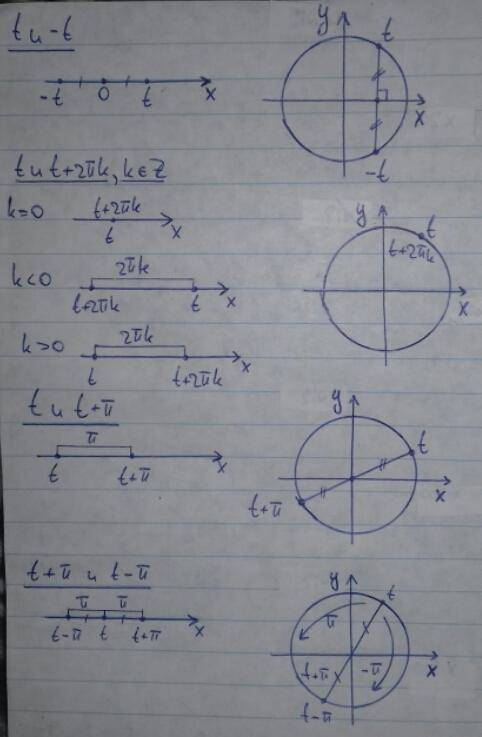
На числовой прямой:
t и -t
Числа имеют противоположные знаки и |t| = |-t|. Точки симметричны относительно нуля.
t и 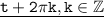
k=0 ⇒ точки совпадают.
k<0 ⇒ t правее t+2πk на 2πk
k>0 ⇒ t левее t+2πk на 2πk.
t и t+π
t левее t+π на π.
t+π и t-π
t+π правее t-π на 2π.
На числовой окружности:
t и -t
Точки симметричны относительно оси абсцисс (Ox).
t и 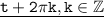
Точки совпадают т.к. 2π это целый круг.
t и t+π
Точки симметричны относительно начала координат т.к. π это половина круга.
t+π и t-π
Точки совпадают т.к. они различаются на 2π, а это целый круг.
Відповідь: 0
Пояснення: фото