Арифмети́ческая прогре́ссия — числовая последовательность вида. , то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d.
Найдем постоянное число d== 6,5.
а3=2,5+6,5=9.
а4=9+6,5=15,5.
Сумма первых 4-х членов=a1+a2+a3+a4=-4+2,5+9+15,5=13
Если тиорема Виета не то действуем в лоб 1 шаг: Первое выражение делим на 2. Второе неизменно x+y=13 x*y=42. 2 шаг: В первом выражении виажаем любую из переменных(допустим это будет икс. Это роли не играет). Второе оставляем неизменным х=(-у)+13 x*y=42 3 шаг: Подставляем полученуую выраженную переменную во второе х=(-у)+13 ((-у)+13)*у=42 4 шаг: Расрываем скобки и переносим число из правой части в левую, приравнивая к нулю х=(-у)+13 -у^2+13у-42=0 5 шаг. Придётся ненадоло забыть про систему и решать вне её.
Вспоминаем общий вид квадратного уравнения a*x^2+b*x+c Отсюда выводим коэффиценты а, b и с а=(-1) b=13 с=(-42) Ну а дальше по формуле дискриминанта находим корни D^2 = b^2-4*a*c Х(первый )= (-b+D)/2a Х(второй) = (-b-D)/2a Для данного получается... D^2 = 13^2-4*(-1)*(-42) = 169-4*42- 169-168=1 Корень из 1 равень 1 Х(первый )= (-13+1)/2*(-1) = (-12)/(-2) = 6 Х(второй) = (-13-1)/2*(-1) = (-14)/(-2) = 7 6 шаг: Вспоминаем про систему и подставляем полученное значение переменной икс в любое из начальных значений системы: 2 (x+y)=26 x*y=42 Тут - то и молучается ответ двумя системами. Х=6, У=7 Х=7, У=6
a3= 9, а4=15,5. Сумма=13
Объяснение:
Арифмети́ческая прогре́ссия — числовая последовательность вида. , то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d.
Найдем постоянное число d=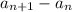 = 6,5.
= 6,5.
а3=2,5+6,5=9.
а4=9+6,5=15,5.
Сумма первых 4-х членов=a1+a2+a3+a4=-4+2,5+9+15,5=13