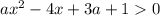
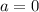квадратное неравенство вырождается в линейное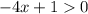
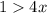
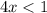
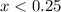
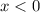
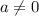
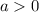
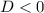) - отлично, график параболы выше оси Ох - неравенство выполняется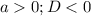
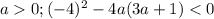
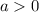
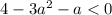
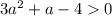
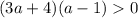
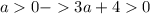авмтоматически
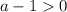или 
- 
; 
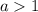
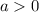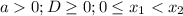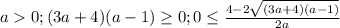
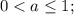- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)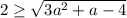
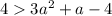
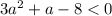- что очевидно верно при условиях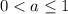 
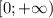
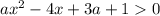
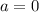квадратное неравенство вырождается в линейное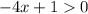
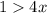
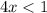
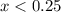
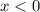
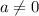
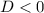) - отлично, график параболы выше оси Ох - неравенство выполняется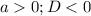
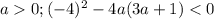
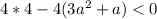
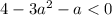
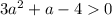
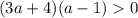
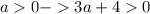авмтоматически
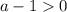или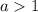 
- 
; 
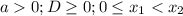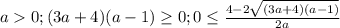
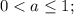- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)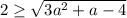
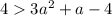
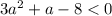- что очевидно верно при условиях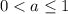 
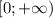
x1= 2, x2= -4, x3= -1+√5, x4= -1-√5
Объяснение:
пусть x²+2x-5=t, тогда
t²-2t-3=0
D= 4+12= 16
t1= (2+4)/2= 3
t2= (2-4)/2= -1
1) x²+2x-5=3
x²+2x-8=0
D= 4+32=36
x1= (-2+6)/2= 2
x2= (-2-6)/2= -4
2) x²+2x-5= -1
x²+2x-4=0
D= 4+16=20
x3= (-2+2√5)/2= -1+√5
x4= (-2-2√5)/2= -1-√5