Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
№1 а
№2 а) (9/2; 10)
б) (54/37; 34/37)
Объяснение:
№1
а)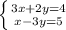
3(5+3y) +2y = 4
15+9y+2y=4
15+11y=4
11y=-11
y= -1
x= 5+3*(-1) = 2
ответ: (2; -1)
б)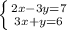
2x-3(6-3x) = 7
2x-18+9x = 7
-18+11x = 7
11x = 25
x = 25/11
y = 6-3* (25/11) = -(9/11)
ответ: (25/11 ; - 9/11)
Нам подходит только система под буквой А
( ты можешь просто подставить (2; -1) в системы и сразу получить результат, но я не знаю, разрешают вам так делать или нет, поэтому расписала системы )
№2
а)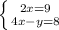
4* 9/2 -y = 8
2*9-y = 8
18-y = 8
y = 10
ответ: (9/2; 10)
б)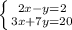
3x+17(-2+2x) = 20
3x-34+34x = 20
37x-34 = 20
37x = 54
x = 54/37
y = -2+2* (54/37) = -2 + 108/37 = 34/37
ответ: (54/37; 34/37)