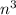 , по условию
, по условию 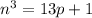 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
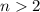 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 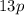 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 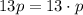 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 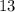 и
и 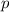 , либо
, либо 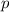 и
и 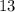 .
.
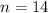 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 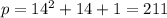 .
.  - действительно простое число, так что
- действительно простое число, так что 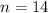 нас устраивает.
нас устраивает.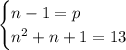
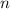 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 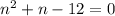 , у которого только один натуральный корень
, у которого только один натуральный корень 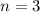 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 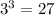
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта (математики ввели себе такой термин для упрощения решения квадратных уравнений). По мимо этого, корни можно найти по теореме Виета, но вот доказать, имеет ли уравнение корни или нет по ней, к сожалению, нельзя.
Формула дискриминанта: D=b²-4ac,
откуда a,b, с - это коэффициенты из уравнения.
Если D>0 (положительный), то уравнение имеет два корня.
Если D=0, то один корень.
Если D<0 (отрицательный), то уравнение корней не имеет.
Поэтому всё задание сводится к нахождению дискриминанта:
x²-10x+27=0
a=1 (если возле переменной не стоит никакое число (например, 2, 3, -10 и т.д.), то подразумевается, что там спряталась единица)
b=-10
c=27
Подставим эти коэффициенты в формулу дискриминанта.
D=(-10)²-4×27×1=100-108=-8 (число -8 отрицательное, поэтому уравнение корней не имеет)
x²+x+1=0
a=1, b=1, c=1
D=b²-4ac=1²-4×1×1=1-4=-3 (-3 отрицательное число, поэтому уравнение корней не имеет)