11 км/час
Объяснение:
Пусть скорость велосипедиста из п. А в п. В составляла х км/час , тогда скорость велосипедиста из п. В в п.А будет ( х+4) км/час .
Время , которое затратил велосипедист на дорогу из п.А в п.В составило 77/х час.,а время на обратный путь ( с учетом 4-х часовой остановки) будет : (77/(х+4))+4 час. Поскольку расстояние одинаковое , можем составить уравнение:
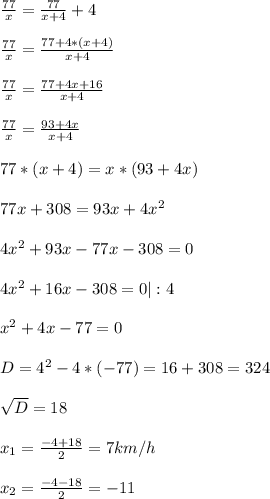
корень х₂ не подходит , поскольку отрицательный , значит скорость велосипедиста из п.А в п.В была - 7 км/час , а на пути из п.В в п.А:
7+4= 11 км/час
Чтобы решать такие задания, тебе нужно просто перетаскивать числа с "x" в левую часть, а без "x" в правую. Потом подсчитать, сколько получится в левой и правой частях. Затем делить обе части на число, которое стоит перед X. Если делишь или умножаешь на положительное число, знаки не меняются. Если делишь или умножаешь на отрицательное число, знаки меняются на противоположные( К примеру 5x = -2 | :5 , x = -2/5 = -0,4. А -10x = 5 | :(-10) , x = -5/10 = -1/2 = -0,5)
При переносе числа из одной стороны в другую, знак меняется на противоположный ( К примеру 5x - 3 = -10x. Если перенесём "-10x" влево, а "-3" вправо, то получим : 5x + 10x = 3)
№606. 6x = x -2
6x - x = -2
5x = -2 | :5
x = -2/5 = -0,4
№608. 5x - 3 = -10x
5x + 10 x = 3
15x = 3 | :15
x = 3/15 = 1/5 = 0,2
№610. 3x - 8 = -x
3x + x = 8
4x = 8 | :4
x = 2
№612. -5x = 5x - 6
-5x - 5x = -6
-10x = -6 | :(-10)
x = 6/10 = 3/5 = 0,6
№614. -6x - 5 = 4x
-6x - 4x = 5
-10x = 5 | :(-10)
x = -5/10 = -1/2 = -0,5
№616. -7x + 8 = 9x
-7x - 9x = -8
-16x = -8 | :(-16)
x = 8/16 = 1/2 = 0,5
№618. -9x - 8 = -8x
-9x + 8x = 8
-x = 8 | :(-1)
x = -8
№620. -5x+2 = -10x
-5x + 10x = -2
5x = -2 | :5
x = -2/5 = -0,4
№622. -4x = -10x - 9
-4x + 10x = -9
6x = -9 | :6
x = -9/6 = -3/2 = -1,5
№624. -1 + 2x = 10x + 3
2x - 10x = 3 + 1
-8x = 4 | :(-8)
x = -4/8 = -1/2 = -0,5
№626. 9 + 4x = 8x - 9
4x - 8x = -9 - 9
-4x = -18 | :(-4)
x = 18/4 = 9/2 = 4,5
№628. 6 - 2x = 3x - 10
-2x - 3x = -10 - 6
-5x = -16 | :(-5)
x = 16/5 = 3,2
ответ:1)Алгебраической называют дробью.
2)Тождество — это уравнение, которое удовлетворяется тождественно
3)число n (показывающее сколько раз повторяется множитель) – показателем степени
4)Квадратное уравнение называют приведенным, если его старший коэффициент равен 1.
5)Решить уравнение - значит найти все его корни или установить, что их нет.
6)Деление числителя и знаменателя на их общий делитель, отличный от
единицы, называют сокращением дроби.
7)при умножении ( делении ) числителя и знаменателя на одно и то же выражение ( число) получившаяся дробь = исходной
8)числители перемножаются отдельно
отдельно знаменатели
полученную дробь если это возможно сокращают
пример
2/3* 3/4 = (2*3)/(3*4)=6/12=1/2 (произвели сокращение на 6
9)Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
10) Сложение и вычитание алгебраических дробей c одинаковыми
знаменателями выполняется по тому же правилу, что и с обыкновенными
дробями:
аd + bd – cd = a+b−cd .
11) Нам известно, что дробь 34 равна частному 3 : 4 ,
значит, выражение ( 14+ 15) : ( 13− 16) = ( 14+ 15)( 13− 16) .
Частное двух чисел или выражений, в котором знак деления
обозначен чертой, называют дробным выражением.
Найдем значения выражений:
а) ( 14+ 15)( 13− 16) = ( 520+ 420)( 26− 16) = ( 920)( 16) = 920 : 16 =
= 920• 61 = 5420 = 2 710 = 2,7
12)Пусть a0 и a1 - натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида [1] последовательного деления с остатком: a0=a0a1+a2, a1=a1a2+a3, a2=a2a3+a4, … ,где натуральные числа a0,a1,a2, … суть неполные частные. Это алгоритм разложения числа a =a0/a1 в правильную цепную дробь, и он применим к любым вещественным числам a. При этомa0=[a], где [a] - целая часть числа a, a1=[1/(a-a0)], … , т.е.
a=a0+ 1a1+ 1a2+ 1a3+ ···,
13)http://school.xvatit.com/images/9/92/11-06-34.jpg
14)Складываются показатели степеней при УМНОЖЕНИИ степеней с одинаковыми основаниями.
2^3+2^5=8+32=40.
Подробнее - на -
Объяснение: