Question

2. построить график функции у = - х2 + 2х + 3. по графику выяснить: 1) при каких значениях х функция принимает положительные значения; 2) при каких значениях х функция убывает; 3) при каких значениях х функция принимает наименьшее значение и найти это значение.

Answer 1

Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).

$x_v=\frac{-b}{2a}=\frac{-2}{-2}=1\\y_v=-1^2+2*1+3=4$

Это координаты вершины, почему именно такие? Корни уравнения:

$\frac{-bб\sqrt{D} }{2a}$, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.

Найдём нули функции:

$D=4+12=4^2;x=\frac{-2б4}{-2} ;\\x_1=3;x_2=-1$

Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.

И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: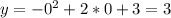 $y=-0^2+2*0+3=3$ то есть (0;3)

1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения

При x∈(-1;3) функция принимает положительные значения

2) При x∈(-∞;1) функция растёт

При x∈(1;+∞) функция убывает

3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)

Максимальное значение 4, достигается в точке (1;4)