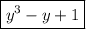Ну насчет столбиком шутки шутками, а ведь можно делить многочлен на многочлен уголком, только в LaTeX это особо не распишешь. А вот разложить на множители вполне можно.
Сначала займемся числителем:
Здесь часто использовался метод искусственного добавления и вычитания слагаемых для вынесения за скобки общих множителей (в виде скобок). Вот каких - дело опыта, но имея опыт с нахождением корней многочленов высоких степеней, я уже знал, конечно, что в разложении будут присутствовать скобки и и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.
Ну насчет столбиком шутки шутками, а ведь можно делить многочлен на многочлен уголком, только в LaTeX это особо не распишешь. А вот разложить на множители вполне можно.
Сначала займемся числителем:
Здесь часто использовался метод искусственного добавления и вычитания слагаемых для вынесения за скобки общих множителей (в виде скобок). Вот каких - дело опыта, но имея опыт с нахождением корней многочленов высоких степеней, я уже знал, конечно, что в разложении будут присутствовать скобки и
и  и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.
и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.
Получили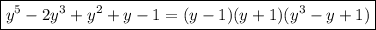
Теперь знаменатель: по известной формуле
получаем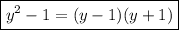
Осталось все это написать вместе и сократить
Сокращать можно только учитывая ограничения
ответ: