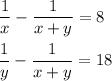
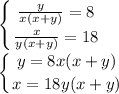
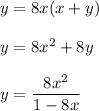
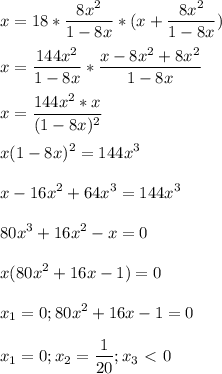

х - дней, 2 слесаря выполнят работу совместно.
х+8 дней - выполняет всю работу 1-й слесарь
х+18 дней - выполняет всю работу 2-й слесарь
1/х - работы выполнят 2 слесаря совместно за день
1/(х+8) - выполнит свою часть работы 1-й слесарь
1/(х+18) - выполнит свою часть работы 2-й слесарь
1/х=1/(х+8)+1/(х+18)
1/(х + 8) + 1/(х + 18) = 1/х
(х + 18 + х + 8)/(х + 8)(х + 18) = 1/х
(2х+26)/х²+8х+18х+144)=1/х
(2х+26)/(х²+26х+144)=1/х
Согласно правилу пропорции:
х*(2х+26)=х²+26х+144
2х²+26х-х²-26х=144
х²=144
х=12 дней - сделают работу совместно
1)x∈(-∞, 1)
2)х∈[-2,5, +∞)
3) х∈[0,4, +∞)
4)х∈[-1,4, +∞)
5) х∈(-∞, 1]
6)х∈(-∞, -8)
Объяснение:
Решить неравенства:
1) 1 + 6х < 7;
6x<7-1
6x<6
x<1
x∈(-∞, 1)
Решения неравенства находятся в интервале при х от
- бесконечности до 1. Неравенство строгое, скобки круглые.
2) 3 – 2х ≤ 8;
-2x<=8-3
-2x<=5
x>= -2,5 знак меняется
х∈[-2,5, +∞)
Решения неравенства находятся в интервале при х от -2,5 до
+ бесконечности. Неравенство нестрогое, скобка квадратная, так как -2,5 входит в число решений неравенства.
3) 9х ≥ 4х + 2;
9x-4x>=2
5x>=2
x>=0,4
х∈[0,4, +∞)
Решения неравенства находятся в интервале при х от 0,4 до
+ бесконечности. Неравенство нестрогое, скобка квадратная, так как 0,4 входит в число решений неравенства.
4) – ( 2х + 1) ≤ 3(х + 2 );
-2x-1<=3x+6
-2x-3x<=6+1
-5x<=7
x>= -7/5 >= -1,4 знак меняется
х∈[-1,4, +∞)
Решения неравенства находятся в интервале при х от -1,4 до
+ бесконечности. Неравенство нестрогое, скобка квадратная, так как -1,4 входит в число решений неравенства.
5) (1+6х)/7 ≤ 1;
1+6x<=7
6x<=7-1
6x<=6
x<=1
х∈(-∞, 1]
Решения неравенства находятся в интервале при х от
- бесконечности до 1. Неравенство нестрогое, скобка квадратная, так как 1 входит в число решений неравенства.
6) 3х/4 - х ˃ 2
3x-4x>8
-x>8
x< -8
х∈(-∞, -8)
Решения неравенства находятся в интервале при х от
- бесконечности до -8. Неравенство строгое, скобки круглые.