1. Укажите взаимное расположение прямых , заданных
уравнениями 4х+3у=2 и 8х-3у=1. Сделайте чертеж
2. Запишите уравнение окружности с центром в точке С(0,5; –1)
и радиусом r = 6
3. Изобразите на координатной плоскости множество точек,
заданное:
а) неравенством y ≥ -2x + 1; б) уравнением y+х^2 – 5=0
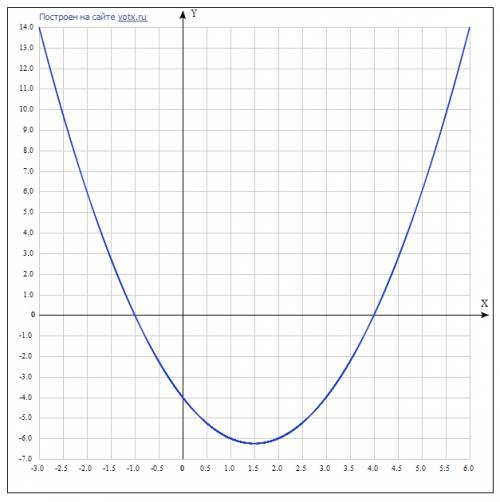
D_f = R \ {5, -2}
f(x) = (x - 4)(x + 1);
f(x) = x^2 - 3x - 4;
Строим график f(x), для этого строим график параболы g(x) = x^2 - 3x - 4, исключаем точки с абсциссами 5 и -2.
Смотрим сколько общих точек может быть у f(x) и h(x) = y = a.
Так как g(5) == g(-2), эти точки нам не подходят, потому что они лежат на одной прямой, и если график h(x) проходит через (5, g(5)), то он проходит и через (-2, g(-2), т.е. не было бы общих точек. Остается вершина параболы x0 = 3 / 2, y0 = g(1.5) = -6,25.
ответ: -6.25.