ДАНО: Y = x² - 4*x - 5.
РЕШЕНИЕ.
Для построения графика применим метод параллельного переноса.
Выделим из функция квадрат суммы аргумента.
Y = x² - 4*x - 5 = (x² - 2*(2*x) + 2²) - 2² - 5 = (x-2)² - 9 - это парабола х² с вершиной в точке А(2; -9).
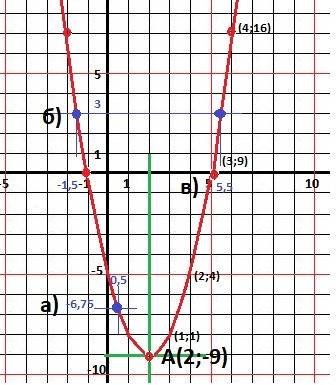
Для построения графика используем значения х²: (0,0), (1,1), (2,4), (3,9), (4,16).
Рисунок с графиком в приложении.
а) По графику находим значение: Y(0.5) ≈ - 6 3/4 ≈ - 6.75
Подставим х = 0,5 и вычисляем: y = 0.5² - 4*0.5 - 5 = 0.25 - 2 - 5 = - 6.75 -точное значение.
б) По графику находим приблизительные значения: х1 = - 1,5 и х2 = 5,5.
Точные значения можно получить решением квадратного уравнения:
х² - 4*х - 5 = 3, D=48, x1 = - 1.46, x2 = 5.46.
в) Точки пересечения с осью Х - корни функции - х1 = -1 и х2 = 5.
Или решив уравнение: Дискриминант - D = 36, √36 = 6, корни х1 = -1 и х2 = 5.
Положительна E(y)>0 при X∈(-∞;-1)∪(5;+∞). Отрицательна - между корнями функции. Отрицательна Е(у)<0 при Х∈(-1;5).
г) Убывает при Х∈(-∞;2) - при Х = 2 - минимум Ymin(2) = -9.
9)2.1/(6.6-2.4)=2.1/4.2=0.5
10)7.2/(8.3-8.6)=-7.2/0.3=-24
11) 9.2/(0.5-2.8)=-9.2/2.3=-4
12)9.4/(4.1+5.3)=9.4/9.4=1
13)(9.5+8.9)/2.3=18.4/2.3=8
14)(6.8-4.7)/1.4=2.1/1.4=1.5
15)(1.7+3.8)/2.2=5.5/2.2=2.5
16)(7.2-6.1)/2.2=1.1/2.2=0.5